Rögzítsük egy l hosszúságú lánc két végét ugyanolyan magasságban, egymástól d távolságra, és mérjük meg a lánc közepének h belógását! Adjuk meg h-t d függvényében! Akasszunk kampós súlyokat a lánc közepére, és mérjük meg, hogyan módosítják ezek h értékét!

A mérés elvégzése során a következõ feladatokat kellett a versenyzõknek megoldani. 1. Megfelelõ (kellõen hajlékony, egyenletes vastagságú, súlyos, de nem nagyon nehéz) lánc választása. Meg kell mérnünk a lánc jellemzõ adatait (a hosszát és a tömegét). A versenyzõk a legváltozatosabb ,,láncokat'' használtak: kutyalánc, ezüstlánc, mûanyaglánc, fürdõszobai mosdó dugóját tartó lánc és megnedvesített spárga egyaránt elõfordult a mérések leírásában. A lánc hosszát mindenki megmérte, a tömegének megadásáról azonban legtöbben megfeledkeztek (pedig a ráakasztott súlyok ,,nagyságát'' érdemes a lánc súlyához viszonyítani).

hosszú vonalzó vagy mérőszalag, lánc, súlyok (rugóra akasztható tömegek)

2. A lánc végeinek rögzítése stabil, de ugyanakkor - legalább az egyik oldalon - könnyen változtatható kell legyen. Voltak, akik két satut, mások egy falécbe (vagy a falba!) vert szögsort, esetleg támlás székeket alkalmaztak. Ügyelnünk kell a két végpont azonos magasságának beállítására és késõbbi ellenõrzésére is. Nagyon feszes lánc (d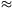l) esetén a felfüggesztési pontoknál jelentõs vízszintes erõk lépnek fel (a székek felborulhatnak, a szögek kiszakadhatnak).

3. A felfüggesztési távolságot és a belógás mélységét sokszor és a lehetõ legpontosabban szeretnénk megmérni, ezért gondoskodnunk kell a könnyû, gyors és pontos leolvasás lehetõségérõl. Azok jártak el a legcélszerûbben, akik (pl. festékkel) megjelölték a lánc közepét, a d és h mennyiségek mérését pedig odaerõsített mérõszalaggal (vonalzóval) oldották meg. A belógás nagyságát mérhetjük a lánc végeit összekötõ (egy léccel vagy fonállal megjelölt) egyenestõl, de kiszámíthatjuk a (kellõen sima) talajtól mért távolságból is.

A mérési elrendezésrõl (a felfüggesztés és a leolvasás módjáról) érdemes valamilyen (vázlatos) rajzot készítenünk, hogy mások is áttekinthessék, maguk elé képzelhessék, saját magunk pedig késõbb felidézhessük, hogy mit is csináltunk.

4. A lánc közepére akasztott súlyok (kampós súlyok, kilós cukor, kólásüveg, karóra stb) tömegét célszerûen a lánc tömegéhez érdemes viszonyítanunk. A nagyon könnyû súly nem okoz észrevehetõ változást a belógásban, a lánchoz képest nagyon nehéz súly pedig teljesen megfeszíti (és deformálja, esetleg el is szakítja) a láncot. Különbözõ tömegû láncokkal és súlyokkal végzett kísérletek eredményeit csak úgy tudjuk összehasonlítani, ha ezeket a súlyadatokat a mérési jegyzõkönyvben rögzítjük.

5. Kellõ számú mérési adat felvétele és áttekinthetõ táblázatban történõ rögzítése. Nem érdemes nagyon kicsiny lépésekben (mondjuk egy l=100 cm hosszú láncnál centiméterenként) változtatni a felfüggesztési pontok távolságát, mert eközben h alig változik, a mérési adatok száma és a mérés ideje pedig indokolatlanul megnõ. Ehelyett érdemes inkább többféle méretû és anyagú lánccal kísérleteznünk, mert ezek ,,független'' információkat ad(hat)nak.

6. A mérési adatokat, azok egymáshoz való viszonyát áttekinthetõ grafikonon is ábrázolnunk kell. Jelen esetben h-t d függvényében vizsgáljuk, különbözõ (esetleg nulla tömegû) nehezékek mellett. Célszerû ezeket az adatsorozatokat (és a ,,szemmel'', vagy számítógéppel rájuk illesztett h(d) függvényeket) ugyanazon milliméterpapíron ábrázolni, mert akkor közvetlenül érzékelhetjük, leolvashatjuk a súlyok által okozott változás jellegét és nagyságát. A különbözõ adatokat (görbéket) különbözõ színnel, vagy más-más jellel (karika, négyzet, csillag, szaggatott vonal stb.) különböztethetjük meg.

Ha van valamilyen ,,elméleti jóslatunk'', azt is rárajzolhatjuk a grafikonra, de jól látható módon különböztessük meg a ténylegesen mért adatoktól, illetve az azokra illesztett görbéktõl. A (lánc tömegéhez képest) nagyon nagy tömegû súly nyilván egyenlõszárú háromszög alakúra feszíti a láncot, s ekkor fennáll a h²+(d/2)²= (l/2)² összefüggés. Ez azt sugallja, hogy érdemes h-t d/2 függvényében ábrázolnunk (vagy ami ezzel egyenértékû: a h-d grafikonon a tengelyek skálabeosztását 2:1 arányban eltorzítanunk), mert ekkor a ,,nagyon nehéz súly'' határesethez tartozó elméleti várakozás egy l/2 sugarú negyedkör lesz. A tényleges mérési adatok eltérése, illetve közeledése ehhez az értékhez a grafikonon jól szemléltethetõ.

Voltak, akik egy külön grafikonon ábrázolták, hogyan függ a h belógás a lánc közepére akasztott G súlytól. Ekkor d rögzített (megadandó) érték, s a különbözõ d-khez tartozó h(G) görbék kerülnek egymás mellé az grafikonon.

7. A mérési adatok hibája egyszerûen a távolságmérés hibája. Ez adódhatott a mérõeszköz pontatlanságából, a leolvasási hibából (parallaxis-hiba), a talaj egyenetlenségeibõl (ha onnan mérjük a lánc belógását) és a láncszemek véges méretébõl származó bizonytalanságból. Gondos kiértékelésnél számításba lehet venni a a felfüggesztési pontok kicsiny magasságkülönbségének lehetõségét és a lánc esetleges megnyúlását is.

• Gnadig Péter