Tömegpont dinamikája » Inga feltekeredése

Média

Filmek

Inga_feltekeredese

Jelenség leírása

Térítsük ki vízszintesig a fonálingát, majd engedjük szabadon mozogni. Amikor a fonál függőleges helyzetbe kerül, az akadály kisebb sugarú körpályára kényszeríti az ingatestet, így a fonál fokozatosan feltekeredik az akadályként szolgáló vékony rúdra.

Összeállítás

Az akadályt állítsuk be úgy, hogy az ingatest negyedkör megtétele után kisebb sugarú körpályára kerüljön. Figyeljünk arra, hogy a körpálya sugara kisebb legyen az eredeti ingahossz 40 %-ánál.

Eszközök

akadályként szolgáló rúd., állvány, Fonál, kisméretű ingatest

Magyarázat

115. Inga feltekeredése

Térítsünk ki vízszintes helyzetig egy fonálingát, majd engedjük el. Amikor a fonál függõleges helyzetbe jut, tehát az ingatest sebessége maximális, a fonál elkezd feltekeredni egy vékony rúdon, ami akadályként a fonál útjában áll, merõlegesen az ingamozgás síkjára. Amint a fonál fokozatosan feltekeredik a rúdra, az ingatest egyre kisebb sugarú körön mozog, átlagos szögsebessége ezért megnõ.

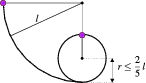
Hol helyezkedhet el az akadály úgy, hogy a fonál sohasem lazuljon meg a mozgás során? Legyen az inga hossza l, majd az akadály kényszerítse r sugarú körpályára az ingatestet. A legkritikusabb pont a körpálya tetõpontja. Ha a fonál éppen a meglazulás határhelyzetében van, akkor a tetõponton az ingatestre csak a nehézségi erõ hat, a nehézségi erõ fedezi a körmozgáshoz szükséges centripetális erõt:

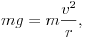
mg=mfrac{v^2}{r},

amibõl kiszámíthatjuk, hogy az r sugarú pálya teljes befutásához a tetõpontban 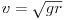v=sqrt{gr} nagyságú sebességre van szükség.

Az energia-megmaradás alapján találhatunk összefüggést a körpálya sugara és a tetõponti sebesség között. A helyzeti energia nulla szintje legyen a pálya legalsó pontjában. Így a kiinduláskor az ingatest mgl helyzeti energiával rendelkezik, az r sugarú körpálya tetõpontjában pedig mg .2r helyzeti energiával és 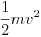frac{1}{2}mv^2 mozgási energiával. Írjuk fel a két állapotra a mechanikai energia-megmaradás tételét, és helyettesítsük be a sebesség értékébe a fenti 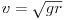v=sqrt{gr} kritikus értéket:

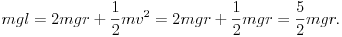
mgl=2mgr+frac{1}{2}mv^2=2mgr+frac{1}{2}mgr=frac{5}{2}mgr.

Az egyenlet elsõ és utolsó tagjának egyenlõségébõl 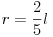r=frac{2}{5}l érték adódik, ami azt jelenti, hogy az akadály nem lehet a pálya aljától számítva 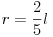r=frac{2}{5}l-nél magasabban, ha azt várjuk el, hogy a fonál sohasem lazuljon meg a mozgás során.


Szerzők

  • Baranyai Klára
  • Honyek Gyula

Forrás, irodalom, hivatkozás

  • Fizika, középiskolai tankönyvsorozat a Műszaki Kiadó gondozásában Szerzők: Gulyás János, Honyek Gyula, Markovits Tibor, Szalóki Dezső, Tomcsányi Péter, Varga Antal
  URI STRING  
/show/115/F-B-C
  CLASS/METHOD  
show/index
  MEMORY USAGE  
610,312 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0003
Controller Execution Time ( Show / Index )  0.0062
Total Execution Time  0.0065
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0004   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('112e93d336a9faf7ea30687626ea9049', '18.224.65.198', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1732411283) 
0.0005   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0004   SELECT *
FROM (`experiments`)
WHERE `eid` = '115' 
0.0003   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '115' 
0.0004   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '115' 
0.0002   SELECT `name`
FROM (`materials`)
WHERE `eid` = '115' 
0.0004   SELECT `source`
FROM (`sources`)
WHERE `eid` = '115' 
0.0005   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '115' 
0.0004   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '115'