Tömegpont dinamikája » Rugóállandó mérése

Média

Filmek

Rugoállandó_mérése

Jelenség leírása

A rugóállandót meghatározhatjuk a rugó sztatikus deformációja alapján (sztatikus módszer), illetve a rugóra akasztott testek rezgésének periódusidejéből is (dinamikus módszer).

Összeállítás

A rugót függőlegesen felfüggesztjük, és a rugó aljára különböző ismert tömegeket akasztunk.

Eszközök

állvány, hosszú vonalzó, mérleg., stopper, súlyok (rugóra akasztható tömegek), Tekercsrugó

Magyarázat

114. Rugóállandó mérése

A rugóállandót megmérhetjük sztatikus és dinamikus módon is. A sztatikus mérésnél lényegében azt vizsgáljuk, hogy bizonyos terhelések hatására mekkora deformációval reagál a rugó. A dinamikus mérés esetén azt mérjük, hogy mekkora periódusidejû rezgéseket végez a rugó, ha különbözõ tömegeket erõsítünk rá.

A rugóállandót sztatikus módszerrel a definiáló egyenlet (Hooke-törvény) alapján mérhetjük meg:

F=Dx,

ahol F a rugót feszítõ erõ, x a rugó megnyúlása, D pedig a rugóállandó. Ha a rugót függõlegesen felfüggesztjük, és a rugó aljára különbözõ ismert tömegeket akasztunk, akkor a rugót feszítõ erõt F=mg alakban adhatjuk meg. Ilyen módon a rugóállandót a

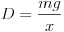
D=frac{mg}{x}

összefüggés alapján számíthatjuk ki.

Pontosabbá tehetjük a mérést (a mérés relatív hibáját 1% alá csökkenthetjük), ha több mérést végzünk, és ábrázoljuk a rugó x megnyúlását az aljára akasztott m tömeg függvényében. A grafikonon megjelenített pontokra jó közelítéssel egyenest illeszthetünk, amelynek meredeksége:

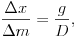
frac{Delta x}{Delta m}=frac{g}{D},

amibõl a rugó D rugóállandója kifejezhetõ.

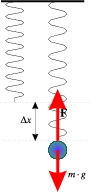
Megjegyzés: Vannak olyan rugók, amelyekben alapállapotban mechanikai összehúzó feszültség van, így csak bizonyos terhelés elérése után kezdenek nyúlni. Az ideális rugókra jellemzõ lineáris erõtörvény alapján a húzóerõ és a megnyúlás nulla szintjét tetszõlegesen választhatjuk meg, ezért nem szükséges a mérést a rugó terheletlen állapotában kezdeni, hanem a lineáris szakasz bármely pontját választhatjuk nulla-szintnek. Ezzel a módszerrel a megnyúlás-terhelés grafikon egyenese mindig áthalad az origón.

A rugóállandó dinamikus mérése a rugóra akasztott test rezgésidejének mérésén alapszik. Jól ismert, hogy a D rugóállandójú rugóra akasztott m tömegû test rezgésideje:

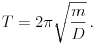
T=2pisqrt{frac{m}{D}},.

A rezgésidõ képletébõl meghatározhatjuk a rugóállandót:

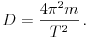
D=frac{4pi^2m}{T^2},.

A sztatikus és a dinamikus mérést összehasonlítva gyakran azt tapasztalhatjuk, hogy a kétféle módszerrel kapott eredmény jelentõsen eltér egymástól. Az eltérés oka az, hogy a rezgésben a rugóra akasztott test mellett a rugó saját tömege is részt vesz, a rugó menetei kisebb-nagyobb mértékben rezegnek. A függõleges helyzetû rugó legfelsõ pontja egyáltalán nem mozog, a legalsó pontja pedig együtt mozog a rugóra akasztott testtel. Ezért a fenti képletben az m tömeghez hozzá kell adnunk valamennyit, amit a rugó effektív tömegének nevezünk, és meff-vel jelölünk.

A rugó effektív tömegét kísérletileg a következõképpen határozhatjuk meg. Végezzünk rezgésidõ méréseket különbözõ tömegekkel. Ábrázoljuk a rezgésidõ négyzetét a rugóra akasztott tömeg függvényében. Ha a fenti képlet érvényes lenne, vagyis a rezgésidõ négyzete egyenesen arányos lenne a rugóra akasztott tömeggel (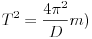T^2=frac{4pi^2}{D}m), akkor az ábrázolás origón átmenõ egyenest mutatna, melynek meredeksége 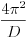frac{4pi^2}{D}. A mérést elvégezve azt tapasztaljuk, hogy az ábrázolt pontok valóban egyenesen fekszenek, azonban az egyenes nem megy át az origón, hanem a pontokra fektetett egyenes valamilyen negatív tömeg értéknél metszi a vízszintes tengelyt. Ez a metszéspont éppen az effektív tömegnek felel meg. Ha ezzel a tömegértékkel vízszintes irányban eltoljuk a függvényt, vagyis az m 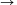om+meff függvény-transzformációt hajtjuk végre, akkor a 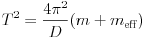T^2=frac{4pi^2}{D}(m+m_{ m eff}) függvénykapcsolat már valóban egyenes arányosságot, origón átmenõ egyenest mutat. Természetesen ennek a párhuzamosan eltolt egyenesnek is ugyanakkora a meredeksége, amibõl a kiszámított D rugóállandó nagy pontossággal megegyezik a sztatikus módszerrel kapott rugóállandóval.

A rezgésidõ mérések azt mutatják, és az elméleti közelítõ számítások is megerõsítik, hogy a rugó effektív tömege nagyjából megegyezik a valódi rugótömeg egyharmad részével: 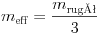m_{ m eff} =frac{m_{ ext{rugó}}}{3}. Mérleg segítségével meggyõzõdhetünk arról, hogy a grafikonról leolvasható effektív rugótömeg valóban jó közelítéssel megegyezik a rugó tömegének egyharmadával. Így végül is arra a következtetésre jutottunk, hogy a rugóra akasztott test rezgésidejének meghatározására szolgáló formula ilyen módon finomítható:

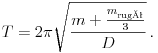
T=2pisqrt{frac{m+frac{m_{ ext{rugó}}}{3}}{D}},.

Ha a rugó tömege elhanyagolható a rugóra akasztott tömeghez képest, akkor várakozásaink szerint visszakapjuk a régi, jól ismert formulát.


Szerzők

  • Baranyai Klára
  • Honyek Gyula

Forrás, irodalom, hivatkozás

  • Fizika, középiskolai tankönyvsorozat a Műszaki Kiadó gondozásában Szerzők: Gulyás János, Honyek Gyula, Markovits Tibor, Szalóki Dezső, Tomcsányi Péter, Varga Antal
  URI STRING  
/show/114/F-B-C
  CLASS/METHOD  
show/index
  MEMORY USAGE  
623,288 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0006
Controller Execution Time ( Show / Index )  0.0105
Total Execution Time  0.0112
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0007   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('6e1d73f6fcaded7c32273d735de89a5d', '18.227.114.125', 'claudebot', 1713484077) 
0.0007   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0008   SELECT *
FROM (`experiments`)
WHERE `eid` = '114' 
0.0009   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '114' 
0.0007   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '114' 
0.0006   SELECT `name`
FROM (`materials`)
WHERE `eid` = '114' 
0.0006   SELECT `source`
FROM (`sources`)
WHERE `eid` = '114' 
0.0005   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '114' 
0.0007   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '114'