Filmek

Ha bizonyos magasságból vízszintes talajra ejtünk labdákat, akkor azok kisebb sebességgel pattannak vissza, mint a leérkezési sebességük. Ha azonban két labdát egymás tetejére helyezünk, és így ejtjük le őket, akkor a felső labda meglepően magasra pattanhat.

Helyezzük a könnyebb labdát a nehezebb tetejére és ejtsünk le a labdákat bizonyos magasságból vízszintes talajra. Vizsgáljuk meg, hogy milyen magasra pattannak vissza.

Labdák (például gumilabda és ping-pong labda).

112. Két labda felpattanása

Ejtsünk labdákat bizonyos magasságból vízszintes felületre. A labdák sohasem pattannak vissza tökéletesen rugalmasan, a visszapattanó labda alacsonyabb magasságot ér el, mint ahonnan elengedtük. Ha két labdát egymás tetejére teszünk, és elengedünk, akkor a felsõ labda sokkal magasabbra emelkedik a visszapattanás után, mint ahonnan indultak. Ennek az a feltétele, hogy az alsó labdának nagyobb tömegûnek kell lennie, mint a felsõnek.

A jelenség magyarázata az, hogy a visszapattanáskor egymás utáni ütközések sorozata játszódik le; elõször az alsó labda ütközik a talajjal, és valamekkora sebességgel elindul felfelé, majd a lefelé mozgó felsõ labda ütközik a már felfelé mozgó alsólabdával. Mivel az alsó tömege nagyobb a felsõénél, az alsó labda egy ütõhöz hasonlóan fellövi a könnyû felsõ labdát.

Tételezzük fel, hogy a labdák tökéletesen rugalmasak, az egymást követõ ütközések pillanatszerûek, és számítsuk ki a visszapattanás utáni sebességüket. Legyen a felsõ labda tömege m, az alsóé km, és érkezzenek a talajra v sebességgel. Tegyük fel, hogy az alsó labda tömege nagyobb (k >1). Tekintsük a függõlegesen felfelé mutató irányt pozitívnak, és tételezzük fel, hogy a labdák mindvégig ugyanazon függõleges egyenes mentén mozognak.

Az elsõ ütközést követõen az alsó labda +v sebességgel mozog felfelé, a felsõ pedig -v sebességgel lefelé. Írjuk fel a lendület- és az energia-megmaradás törvényét a második ütközésre: kmv-mv& =kmv_a +mv_f kmv²/2+mv²/2=kmv_a²/2+mv_f²/2, ahol v_a-val és v_f-fel jelöltük a labdák felpattanás utáni sebességeit. Az egyenletrendszer fizikailag értelmes megoldása: v_a =((k-3)/(k+1))v és < v_f =((3k-1)/(k+1))v. Ha az alsó labda háromszoros tömegû (k = 3), akkor visszapattanás után az alsó labda megáll (v_a = 0), és a felsõ labda kétszeres sebességgel pattan fel (v_f = 2v), így négyszeres magasságra pattan fel. Ebben az esetben a rendszer teljes mozgási energiáját a felsõ labda kapja meg (negyedakkora tömeg négyszeres energiát kap). Érdekes észrevenni azonban, hogy nem ez a tömegarány jelenti a legmagasabb felpattanást; minél nagyobb az alsó labda tömege a felsõhöz képest, annál inkább növekszik a felsõ labda végsõ sebessége, és határátmenetben v_f 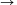3v, ha k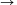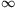, vagyis a felsõ labda sebessége háromszorosnál jobban nem nõhet, legfeljebb kilencszeres magasságra pattanhat vissza.

Érdemes még megvizsgálni a k = 1 határesetet is. Ekkor v_a=-v és v_f=v, ami azt jelenti, hogy az alsó labda újra a talajjal ütközik, majd rögtön felpattan v sebességgel, és a két azonos tömegû labda lényegében együtt mozog felfelé, mintha csak egy testet ejtettünk volna le. Minden egyéb esetben (k > 1) a felsõ labda lesz gyorsabb. Az alsó labda a második ütközés után vagy felfelé indul (k> 3), vagy megáll (k = 3), vagy lefelé mozdul el (3 >k> 1), ám ebben az esetben a talajjal történõ ütközés megváltoztatja a sebességének az irányát. Mindezeket figyelembe véve a probléma teljes megoldása k 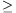1 esetén: v_a =|(k-3)/(k+1)|v, és v_f = 3k-1k+1v.

Megjegyzés: Ha a tömegarányra vonatkozó k 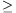1 feltétel nem teljesül, vagyis 0< k <1, akkor az alsó labda lesz gyorsabb, és gyors pattogás kezdõdik a felsõ labda és a talaj között. Ekkor már nem tartható a tökéletesen rugalmas ütközést feltételezõ közelítés, gyors energiaveszteség következik be, és a megfigyelésekkel egyezõen a labdák alig pattannak fel.

• Baranyai Klára
• Honyek Gyula

• Fizika, középiskolai tankönyvsorozat a Műszaki Kiadó gondozásában Szerzők: Gulyás János, Honyek Gyula, Markovits Tibor, Szalóki Dezső, Tomcsányi Péter, Varga Antal