Pontrendszerek » Rugalmas ütközés

Média

Filmek

Rugalmas_ütközés

Jelenség leírása

Ha az álló céltárgy és a lövedék tömege megegyezik, akkor az ütközés után a lövedék megáll, és a céltárgy ugyanakkora sebességgel mozog, mint amennyivel a lövedék becsapódott. Ha a lövedék tömege nagyobb a céltárgy tömegénél, akkor az ütközés után mindkét test ugyanabba az irányba mozog tovább, mint amilyen a lövedék eredeti sebessége volt. Ha a céltárgy tömege nagyobb a lövedék tömegénél, akkor a lövedék visszapattan a céltárgyról.

Összeállítás

Helyezzünk vízszintes sínre álló kiskocsit (céltárgy) és ütköztessünk neki rugós ütközővel ellátott másik kiskocsit (lövedék). Több kocsi egymásra helyezésével változtassuk a lövedék, illetve a céltárgy tömegét.

Eszközök

egyforma kiskocsik rugós ütközőkkel., Vízszintes sín

Magyarázat

107. Rugalmas ütközés

Tökéletesen rugalmas ütközésekkor az impulzus (lendület) megmaradásán kívül a mozgási energia megmaradása is érvényes, vagyis a testek ütközés elõtti lendületének, illetve mozgási energiájának összege megegyezik a testek ütközés utáni lendületének, illetve mozgási energiájának összegével.

A következõkben kizárólag olyan egyenes és centrális tökéletesen rugalmas ütközésekre szorítkozunk, amikor a céltárgy kezdetben áll. A rugalmas ütközéseket két szakaszra bonthatjuk; az elsõ szakaszban összenyomódás játszódik le, a második szakaszban pedig szétlökõdés. Tökéletesen rugalmas ütközésekkor ugyanolyan erõlökések játszódnak le összenyomódáskor, mint szétlökõdéskor. A két szimmetrikus folyamat között az ütközõ testek azonos sebességgel mozognak egy pillanatra. Ezt a közös sebességet jelöljük c-vel, amit a lendület-megmaradás törvénye segítségével határozhatunk meg:

m1 v=(m1 +m2 )c,

ahol a lövedék tömegét m1-gyel, a céltárgy tömegét pedig m2-vel jelöltük, továbbá v jelöli a lövedék kezdeti sebességét. A lövedék ütközés utáni sebessége legyen v1, a céltárgyé pedig v2.

Az összenyomódás során a céltárgy olyan erõlökést kap, ami sebességét nulláról c-re változtatja. A szétlökõdéskor ez az erõlökés megismétlõdik, vagyis a céltárgy sebessége az ütközés után:

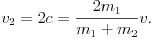
v_2=2c=frac{2m_1}{m_1+m_2}v.

A lövedék esetén összenyomódáskor a sebességváltozás c-v, és ez ismétlõdik meg a szétlökõdéskor, vagyis az ütközés után a lövedék teljes sebességváltozása 2(c-v) lesz. Ennek megfelelõen a lövedék ütközés utáni sebessége:

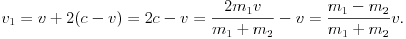
v_1=v+2(c-v)=2c-v=frac{2m_1v}{m_1+m_2}-v=frac{m_1-m_2}{m_1+m_2}v.

Ha a lövedék és a céltárgy tömege megegyezik (m1 =m2), akkor a fenti összefüggések alapján a lövedék ütközés utáni sebességére v1 =0 adódik, illetve a céltárgy sebessége v2 =v lesz, vagyis egyenlõ tömegek esetén sebességcsere játszódik le.

Legyen a lövedék tömege k-szor nagyobb a céltárgyénál (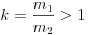k=frac{m_1}{m_2}>1). Ilyenkor a lövedék sebessége az ütközés után 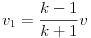v_1=frac{k-1}{k+1}v lesz, illetve a céltárgy 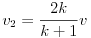v_2 =frac{2k}{k+1}v sebességgel mozog. Vegyük észre, hogy ha a lövedék tömege sokkal nagyobb a céltárgy tömegénél (k 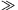gg1), akkor az ütközés után a lövedék lényegében változatlan v1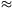approxv sebességgel halad tovább (nem vesz tudomást a könnyû céltárgyról), illetve ekkor a céltárgy közelítõleg v2 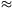approx2v sebességet szerez (mintegy visszapattan a végtelen tömegû lövedékrõl).

!! ewpage!! Végül legyen a céltárgy tömege k-szor nagyobb a lövedékénél (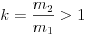k=frac{m_2}{m_1}>1). A behelyettesítést elvégezve ezt kapjuk: v1 =((1-k)/(1+k))v< 1 és v2 =(2/(1+k))v. Láthatjuk, hogy ilyen esetben a könnyû lövedék visszapattan a céltárgyról (v1 ellenkezõ elõjelû, mint v). Ha a céltárgy tömege sokkal nagyobb a lövedékénél, akkor v1 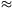approx-v (ilyenkor a lövedék pattan vissza a céltárgyról), illetve v2 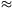approx0 (a kicsiny lövedék alig tudja meglökni a nagy céltárgyat).

Érdekes megfigyelni a lövedék és a céltárgy lendület-változását, amikor a lövedék visszapattan a céltárgyról (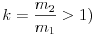k=frac{m_2}{m_1}>1). A lövedék kezdeti lendülete I0 =m1 v, ami I1=m1 v1-re változik, vagyis a lövedék lendület-változása:

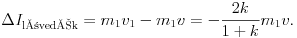
Delta I_{ ext{lövedék}}=m_1v_1-m_1v=-frac{2k}{1+k}m_1v.

Könnyen meggyõzõdhetünk arról, hogy ennek a lendület-változásnak a (-1)-szerese a céltárgy lendülete (illetve egyben lendület-változása is, hiszen a céltárgy állt):

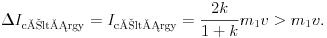
Delta I_{ ext{céltárgy}}=I_{ ext{céltárgy}}=frac{2k}{1+k}m_1v>m_1v.

Mivel k > 1, láthatjuk, hogy a céltárgy nagyobb lendületet kapott, mint amekkorával a lövedék kezdetben rendelkezett. Ennek oka az, hogy a lövedék visszapattan a céltárgyról, tehát lendület-változásának abszolút értéke nagyobb, mint a kezdeti lendületének nagysága. Ha a céltárgy tömege sokkal nagyobb a lövedékénél, akkor a lövedék saját kezdeti lendületének közel kétszeresét adja át a céltárgynak, miközben mozgási energiáját megõrzi. Ha tehát egy labda közelítõleg tökéletesen rugalmasan pattan vissza a talajról, akkor lendületének kétszeresét adja át a Földnek, miközben mozgási energiájára gondosan ügyel, hogy abból szemernyit se veszítsen.


Szerzők

  • Baranyai Klára
  • Honyek Gyula

Forrás, irodalom, hivatkozás

  • Fizika, középiskolai tankönyvsorozat a Műszaki Kiadó gondozásában Szerzők: Gulyás János, Honyek Gyula, Markovits Tibor, Szalóki Dezső, Tomcsányi Péter, Varga Antal
  URI STRING  
/show/107/F-B-D
  CLASS/METHOD  
show/index
  MEMORY USAGE  
623,632 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0003
Controller Execution Time ( Show / Index )  0.0052
Total Execution Time  0.0055
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0004   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('464c892e4d63124ccfe3562452721569', '18.190.28.78', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1713866866) 
0.0004   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0003   SELECT *
FROM (`experiments`)
WHERE `eid` = '107' 
0.0004   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '107' 
0.0005   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '107' 
0.0004   SELECT `name`
FROM (`materials`)
WHERE `eid` = '107' 
0.0004   SELECT `source`
FROM (`sources`)
WHERE `eid` = '107' 
0.0003   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '107' 
0.0003   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '107'