Merev testek mechanikája » Stabilitás a lejtőn

Média

Filmek

Stabilitas_lejton_lassítva

Jelenség leírása

Ha a fahasábok elegendően magasak, illetve a súrlódás elegendően nagy, akkor a hasábok felborulnak a lejtőn. Ha a súrlódást tetszőlegesen lecsökkentjük (a könnyen mozgó kiskocsi segítségével), akkor akármilyen magas hasáb felborulás nélkül, tiszta transzlációs mozgással halad lefelé a lejtőn.

Összeállítás

A fahasábokat egyenként, illetve egymás tetejére állítva a lejtőre helyezzük, majd elengedjük őket. Ugyanezt megismételjük úgy, hogy a fahasábokat a könnyen mozgó kocsira tesszük, és ezt az összeállítást helyezzük a lejtőre.

Eszközök

Hosszú lejtő, két fahasáb, könnyen mozgó kiskocsi.

Magyarázat

106. Stabilitás a lejtõn

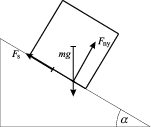
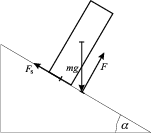
Elõször vizsgáljuk azt az esetet, amikor a súrlódás olyan nagy, hogy a fahasáb nyugalomban maradna a lejtõn, hacsak fel nem borul. Úgy szokás fogalmazni, hogy három erõ hat a fahasábra: a nehézségi erõ, aminek támadáspontja a fahasáb tömegközéppontjában van; a tapadási súrlódási erõ, aminek a hatásvonala a lejtõ és a fahasáb érintkezési felülete mentén halad; valamint a lejtõre merõleges kényszererõ. Közismert, hogy egy test, amelyre három, egy síkban fekvõ erõ hat, akkor van mechanikai egyensúlyban, ha a három erõ eredõje nulla, illetve a három erõ hatásvonala egy ponton megy át. (Ezt a következõ módon magyarázhatjuk meg: A háromból tekintsük két erõ hatásvonalának metszéspontját, amire ez a két erõ nem gyakorol forgatónyomatékot, hiszen erõkarjuk nulla. Így a harmadik erõnek is nulla forgatónyomatékot kell erre a pontra kifejtenie, vagyis a harmadik erõ hatásvonalának is át kell mennie a metszésponton.) Tehát a lejtõre merõleges kényszererõ támadáspontját a nehézségi erõ és a súrlódási erõ hatásvonalainak metszéspontja jelöli ki.

Ha ez a pont a hasáb lejtõvel érintkezõ felületére esik, akkor a fahasáb stabilan áll a lejtõn. Ha viszont a nehézségi erõ hatásvonala a hasáb lejtõvel érintkezõ felületén kívül metszi a lejtõt, akkor a test felborul.

A sztatikus stabilitás után vizsgáljuk meg a dinamikai egyensúlyt is. Ilyenkor azt vizsgáljuk, hogy milyen feltételek teljesülése esetén képes a fahasáb felborulás nélkül (tisztán transzlációs mozgással) lecsúszni a lejtõn. Fontos felhívni a figyelmet arra, hogy gyorsuló mozgás esetén a forgatónyomatékokat a test tömegközéppontjára kell számítanunk.

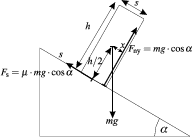
Feltesszük tehát, hogy a test felborulás nélkül a=g(sin 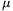alpha-mucos alpha) gyorsulással mozog lefelé a lejtõn. A fahasáb szélessége legyen s, magassága h. A nehézségi erõ (mg) forgatónyomatéka a tömegközéppontra vonatkoztatva nulla. A súrlódási erõ (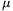mumgcos alpha) forgatónyomatéka: 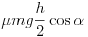mu mgfrac{h}{2}cosalpha. Ezzel a forgatónyomatékkal kell egyensúlyt tartania a felületre merõleges kényszererõ (mgcos alpha) nyomatékának. Szabad paraméterként jelentkezik a felületre merõleges nyomóerõnek a tömegközéppontra vonatkozó erõkarja, amit nevezzünk x-nek. Így a forgatónyomaték egyensúly a következõ alakban írható fel:

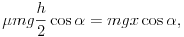
mu mgfrac{h}{2}cosalpha=mgxcosalpha,

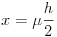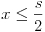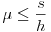amibõl x=mufrac{h}{2}. Az x erõkar értékét viszont a fahasáb szélessége korlátozza: xlefrac{s}{2}, tehát a dinamikai stabilitás feltétele: mulefrac{s}{h}.

Ez azt jelenti, hogy például 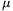mu=0,1 súrlódási együttható esetén egészen addig stabilan (felborulás nélkül) csúszik le a test a lejtõn, amíg magassága tízszer jobban meg nem haladja a szélességét. Érdekes észrevennünk, hogy a dinamikai stabilitás feltétele nem függ a lejtõ hajlásszögétõl. (A sztatikus stabilitás feltétele hajlásszögfüggõ: 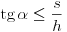mathop{ m tg}alphale frac{s}{h}.) Ugyancsak figyelemreméltó eredmény az is, hogy súrlódásmentes lejtõn (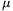mu=0) akármilyen magas fahasáb borulás nélkül csúszik le. Ennek oka az, hogy ilyenkor csak két erõ (nehézségi erõ és felületre merõleges nyomóerõ) hat a testre, melyeknek metszéspontja éppen a tömegközéppont, amelyre tehát nem tudnak forgatónyomatékot kifejteni.


Szerzők

  • Baranyai Klára
  • Honyek Gyula

Forrás, irodalom, hivatkozás

  • Fizika, középiskolai tankönyvsorozat a Műszaki Kiadó gondozásában Szerzők: Gulyás János, Honyek Gyula, Markovits Tibor, Szalóki Dezső, Tomcsányi Péter, Varga Antal
  URI STRING  
/show/106/F-B-E
  CLASS/METHOD  
show/index
  MEMORY USAGE  
623,752 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0007
Controller Execution Time ( Show / Index )  0.0098
Total Execution Time  0.0106
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0006   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('dcc9ba9713b4e0fda505b2f5609665f5', '3.135.194.138', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1732417383) 
0.0006   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0006   SELECT *
FROM (`experiments`)
WHERE `eid` = '106' 
0.0006   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '106' 
0.0006   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '106' 
0.0004   SELECT `name`
FROM (`materials`)
WHERE `eid` = '106' 
0.0004   SELECT `source`
FROM (`sources`)
WHERE `eid` = '106' 
0.0005   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '106' 
0.0006   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '106'