Magnetosztatika » Rúdmágnesek kölcsönhatása

Jelenség leírása

Két rúdmágnes közül az egyiket rögzítjük, a másikat pedig engedjük szabadon forogni a középpontján átmenõ függõleges tengely körül. Tanulmányozzuk a mágnesre ható forgatónyomatékot az elfordulási szög és a mágnesek l távolságának függvényében!

Eszközök

mágnesek, szögmérő, vonalzó

Magyarázat

M. 158. Két rúdmágnes közül az egyiket rögzítjük, a másikat pedig engedjük szabadon forogni a középpontján átmenõ függõleges tengely körül. Tanulmányozzuk a mágnesre ható forgatónyomatékot az \alpha elfordulási szög (0<\alpha<180o) és a mágnesek l távolságának függvényében!

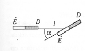
Megoldás. A mérés során a legnagyobb nehézséget a forgó mágnesrúd felfüggesztésének megoldása és a forgatónyomaték pontos mérése okozza. A legcélszerûbb a mágnesrudat az ábrán látható módon egy függõlegesen kifeszített torziós szálra erõsíteni. Ez a megoldás igen érzékeny forgatónyomaték-mérést tesz lehetõvé, és biztosítja, hogy a mágnesrúd csak a szál másik tengelye mentén fordulhasson el. A szál egyik vége legyen rögzített, a szál másik végére pedig szereljünk egy szögbeosztással ellátott forgatható tárcsát. E tárcsát adott szöggel elfordítva a mágnesrúdra (amennyiben a helyzete eközben nem változik) a szögelfordulással egyenesen arányos forgatónyomatékot fejthetünk ki. Az arányossági tényezõt közvetlenül megmérhetjük vagy kiszámolhatjuk a rúdmágnes tehetetlenségi nyomatékának és a torziós rezgések periódusidejének ismeretében, de használhatjuk egyszerûen a torziós szál szögelfordulását mint önkényes forgatónyomaték-egységet.

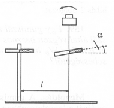
A másik, nem forgó mágnesrudat erõsítsük egy mozgatható állványra, a forgó mágnessel azonos magasságban. A két mágnes középpontjának távolságát jelölje l, a forgómágnes szögelfordulását pedig \alpha. Adott l, \alpha értékek mellett a forgatónyomaték mérésének menete a következõ:

- A forgó tárcsa segítségével állítsuk be a forgó mágnesrúd \alpha szögû helyzetét.

- Helyezzük el az állványon lévõ mágnesrudat a másik mágnestõl l távolságra. (Eközben persze a torziós szálon lévõ mágnes kicsit elfordul.)

- A torziós szálon lévõ tárcsa segítségével állítsuk vissza a forgó mágnest az \alpha szögû helyzetbe. Ehhez a visszaállításhoz szükséges szögelfordulás jellemzi a mágnesre ható M forgatónyomatékot.

Liptai Bernadett (Kazincbarcika, Ságvári E. Gimn., 8. o.t.) ezzel a módszerrel mérte meg különbözõ l és \alpha értékek mellett az M forgatónyomatékot. (Minden esetben három független mérést átlagolt.) Az 1. grafikonon rögzített \alpha érték mellett ábrázolta a forgatónyomaték távolságfüggését, a 2. grafikonon pedig néhány rögzített távolság esetén láthatjuk a forgatónyomaték szögfüggését. (Általános tapasztalat, hogy rögzített l távolság mellett

M(\alpha) = -M(-\alpha) = +M(180o- \alpha),

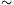így a mérést elegendõ a 0o\le\alpha\le90o tartományban végezni.) Ideális, pontszerû dipólusokra megmutatható, hogy rögzített \alpha esetén M \sim1/l3, míg rögzített l esetén M 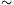\simsin \alpha. Látható, hogy az 1. és 2. grafikonon ábrázolt mérési eredmények jó összhangban vannak a pontszerû dipólusokra vonatkozó elméleti összefüggésekkel.

1. grafikon

2. grafikon

Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Varga István
  URI STRING  
/show/658/F-H-C
  CLASS/METHOD  
show/index
  MEMORY USAGE  
619,808 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0003
Controller Execution Time ( Show / Index )  0.0056
Total Execution Time  0.0059
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0006   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('401a0e8121496b01ef2736e4dedbaeec', '3.141.27.244', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1714062655) 
0.0003   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0004   SELECT *
FROM (`experiments`)
WHERE `eid` = '658' 
0.0006   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '658' 
0.0004   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '658' 
0.0003   SELECT `name`
FROM (`materials`)
WHERE `eid` = '658' 
0.0002   SELECT `source`
FROM (`sources`)
WHERE `eid` = '658' 
0.0003   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '658' 
0.0002   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '658'