Folyadékok és gázok mechanikája » Pingponglabda víz alatt

Jelenség leírása

Egy edény alján kör alakú nyílás van, rajta egy pingponglabda. Ha az edényben elegendõen sok víz van, a labda az edény alján marad. Óvatosan csökkentve a víz mennyiségét, egy bizonyos h vízmagasságnál a pingponglabda felemelkedik. Mérjük meg, hogyan függ h értéke a lyuk átmérõjétõl!

Eszközök

pingponglabda, vizeskád, vonalzó

Magyarázat

M. 156. Egy edény alján kör alakú nyílás van, rajta egy pingponglabda. Ha az edényben elegendõen sok víz van, a labda az edény alján marad. Óvatosan csökkentve a víz mennyiségét, egy bizonyos h0 vízmagasságnál a pingponglabda felemelkedik. Mérjük meg, hogyan függ h0 értéke a lyuk átmérõjétõl!

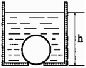
Megoldás. A pingponglabdára a nehézségi erõn és a lyuk pemere által kifejtett kényszererõn kívül a víz nyomásából származó ,,felhajtóerõ'' hat. Ez utóbbi nem számítható olyan egyszerûen, mint a teljes egészében víz alatt levõ testeknél, hiszen a lyuk alatti rész nem érintkezik a vízzel. (A probléma részletesebb elméleti tárgyalását lásd az FN. 2784. feladat megoldásánál, lapunk 283. oldalán!) Azt azonban könnyen beláthatjuk, hogy a h vízmagasság csökkenésével a szokásos felhajtóerõbõl hiányzó rész fokozatosan csökken, tehát a víz által kifejtett (felfelé ható) erõ egyre növekszik. Ha ez az erõ eléri és meghaladja a pingponglabda súlyát, a labda elválik a lyuktól.

A mérés elvégzésekor célszerû átlátszó falú edényt (például mûanyag mérõhengert) használni, ennél a vízszint kritikus magasságát könnyen le tudjuk olvasni. Ügyelnünk kell arra, hogy az edény alján a lyuk sima peremû és minél pontosabban kör alakú legyen, így a mérés közben nem folyhat ki a víz a labda mellett. Célszerû minden lyukméret mellett több mérés eredményét átlagolni, így pontosabban kapjuk meg a kritikus vízmagasság értékét.

Az 1. grafikon Varga Dezsõ (Miskolc, Földes F. Gimn., II. o.t.) mérési eredményeit mutatja, mindegyik pont 6-8 mérés átlaga. Látható, hogy h0 a lyuk sugarának növekedtével erõsen csökken. Elméleti megfontolások szerint (amennyiben elhanyagoljuk az adott átmérõjû pingponglabda vízbe merülõ résztérfogatának a lyuk méretétõl való függését) a kritikus vízmagasság a lyuk területével, vagyis a lyuk sugarának négyzetével fordítottan arányos. A 2. grafikon h0-t 1/r2 függvényében ábrázolja, s a mérési adatok jó közelítéssel egy (az origón átmenõ) egyenesen helyezkednek el.

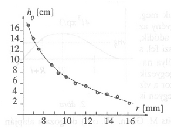
1. grafikon

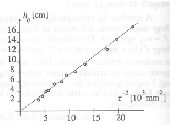
2. grafikon

Érdekes jelenség, hogy amikor a labda kicsit felemelkedik a lyukról és megindul a víz kiömlése, a Bernoulli-törvénynek megfelelõen a lyuk pereme közelében lecsökken a víz nyomása, s emiatt a labda nem tud felemelkedni a víz felszínére. A pontos mérésnél tehát meg kell különböztetnünk a vízfolyás megindulását és a labda felemelkedését.

Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Biró Tibor
  • Varga Dezsõ
  URI STRING  
/show/656/F-B-G
  CLASS/METHOD  
show/index
  MEMORY USAGE  
612,016 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0004
Controller Execution Time ( Show / Index )  0.0090
Total Execution Time  0.0095
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0005   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('ec72052b5389903382e22f03f38cfeed', '3.144.92.165', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1732413018) 
0.0005   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0006   SELECT *
FROM (`experiments`)
WHERE `eid` = '656' 
0.0006   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '656' 
0.0006   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '656' 
0.0004   SELECT `name`
FROM (`materials`)
WHERE `eid` = '656' 
0.0003   SELECT `source`
FROM (`sources`)
WHERE `eid` = '656' 
0.0004   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '656' 
0.0005   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '656'