Jelenség leírása
Konzervesüveg csavaros fedelének közepére fúrjunk kicsiny lyukat. Ütköztessünk egy ilyen korongot vízszintes asztallapon egy ugyanakkora méretû másik, álló korongnak olymódon, hogy a két test különbözõ irányban haladjon tovább. A középpontok kezdeti és végsõ helyzetének ismeretében határozzuk meg, hogy a haladó mozgási energia mekkora hányada veszett el az ütközés során. Vizsgáljuk ezt a mennyiségét a kezdeti sebesség, illetve az ábrán látható b mennyiség (az ún. ütközési paraméter) különbözõ értékeire!
Eszközök
konzervfedők, szögmérő, vonalzó
Magyarázat
M. 154. Konzervesüveg csavaros fedelének közepére fúrjunk kicsiny lyukat. Ütköztessünk egy ilyen korongot vízszintes asztallapon egy ugyanakkora méretû másik, álló korongnak olymódon, hogy a két test különbözõ irányban haladjon tovább. A középpontok kezdeti és végsõ helyzetének ismeretében határozzuk meg, hogy a haladó mozgási energia mekkora hányada veszett el az ütközés során. Vizsgáljuk ezt a mennyiségét a kezdeti sebesség, illetve az ábrán látható b mennyiség (az ún. ütközési paraméter) különbözõ értékeire!
Megoldás. A mérés pontos elvégzéséhez mindenekelõtt a mozgó konzervfedél precíz indításáról kell gondoskodnunk. Biztosítanunk kell, hogy a korong egy elõre meghatározott egyenes mentén mozogjon, és minden mérésnél lehetõleg azonos sebességgel ütközzön a másik korongnak. Ezt a problémát töbféleképpen is megoldhatjuk: indíthatjuk a korongot lejtõrõl, vagy rugó, esetleg gumiszál felhasználásával készíthetünk egy ,,kilövõszerkezetet''.
A b paraméter egy konkrét értéke mellett vegyük fel a két korongnak közvetlenül az ütközés elõtti helyzetét (1. ábra, O1, O2 pont), majd a kísérlet elvégzése után jelöljük meg a korongok végsõ helyzetét (O1', O2' pont)! Az O1O1', ill. az O2O2' szakaszok iránya megadja a testek ütközés utáni sebességének irányát, a szakaszok hossza pedig (egyenletes súrlódást feltételezve) arányos a korongok mozgási energiájával (sebesség-négyzetével).
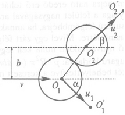
1. ábra
Jelöljük a kilõtt korong ütközés elõtti sebességét v-vel, a korongok ütközés utáni sebességeit u1-gyel, ill. u2-vel, a kilövés irányához képesti eltérési szögeket pedig  -val, ill.
-val, ill. 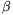 -val. Major Zsuzsanna (Stuttgart, Friedrich-Eugens Gymnasium, II. o.t.) a vizsgálandó relatív mozgásenergia-veszteséget a következõ gondolatmenet alapján fejezte ki a jól mérhetõ
-val. Major Zsuzsanna (Stuttgart, Friedrich-Eugens Gymnasium, II. o.t.) a vizsgálandó relatív mozgásenergia-veszteséget a következõ gondolatmenet alapján fejezte ki a jól mérhetõ  és
és 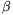 szög segítségével:
szög segítségével:
Az ütközésre érvényes az impulzusmegmaradás, így:
v = u1 cos  + u2 cos
+ u2 cos 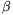 , 0 = u1 sin
, 0 = u1 sin  - u2 sin
- u2 sin 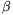 .
.
Innen
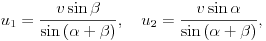
így a mozgási energia relatív vesztesége:
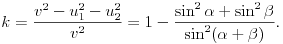
Major Zsuzsanna mérési eredményeit az 1. grafikon tartalmazza. Minden b paraméterértékhez három mérés tartozik, aszerint, hogy v kicsi, közepes vagy nagy. A grafikonról látható, hogy - mérési hibán belül - k értéke nem függ a v kezdeti sebességtõl, azonban k az ütközési paraméter függvényében kb b=2 cm-nél maximumot mutat.
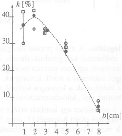
1. grafikon
Megjegyzés. Sok megoldó az ütközést súrlódásmentesnek tekintette, azaz feltételezte, hogy az ütközés alatt a korongok között csak centrális (a felületre merõleges irányú) erõk hatnak. Ezen feltételezés mellett a kezdetben mozgó korongnak az O1O2 egyenesre merõleges sebességkomponense nem változna az ütközés során, a meglökött korong sebessége pedig O1O2 irányú lenne. Azonban néhány kísérletet elvégezve láthatjuk, hogy a korongok az ütközés után forgásba jönnek; ez arra utal, hogy az ütközés során a korongok között a közös érintkezési felülettel párhuzamos irányú súrlódási erõ is fellép. Ez az ütközés elméleti leírását megnehezíti, azonban - mint az láttuk - a mérés az ütközés folyamatának részletes ismerete nélkül is elvégezhetõ.


