Puha fekete ceruzával satírozzunk be egy papíron különbözõ alakú és nagyságú téglalapokat. Mérjük meg a téglalapok elektromos ellenállásait a szemközti oldalaik között! Találunk-e valamilyen szabályosságot?

grafitceruzák, multiméter, müanyagvonalzó

M. 149. Puha fekete ceruzával satírozzunk be egy papíron különbözõ alakú és nagyságú téglalapokat. Mérjük meg a téglalapok elektromos ellenállásait a szemközti oldalaik között! Találunk-e valamilyen szabályosságot?

Megoldás. Néhány próbamérés elvégzése után láthatjuk, hogy a mérés érzékeny arra, hogy milyen vastagon és milyen egyenletesen satíroztuk be a téglalapot. Célszerû emiatt a grafitot a satírozás után egy puha anyaggal szétdörzsölni a felületen, így biztosíthatjuk a grafitréteg egyenletes eloszlását. Érdemes továbbá egyetlen nagyméretû téglalapból kiindulni és ennek a méretét csökkenteni a mérés során, így biztosíthatjuk a legegyszerûbben azt, hogy a különbözõ mérésekhez használt minták közel azonos minõségûek legyenek. Ügyelnünk kell még az elektromos kontaktusok helyes kialakítására is. Mivel a feladat a szemközti oldalak közti ellenállás mérése, ezért a téglalaphoz egy-egy oldala mentén, annak teljes hosszában kell csatlakoztatnunk az elektródákat.

Megyeri Szabolcs (Monor, József A. Gimn. II. o. t.) egy 12 cm-szer 10 cm-es téglalapból indult ki, melynek ellenállását elõször a 10 cm-es oldalak között mérte meg úgy, hogy az elektródákat centiméterenként közelítette egymáshoz. Ezután levágott egy 12 cm hosszú, 1 cm széles csíkot a téglalapból, és az elektródákat centiméterenként közelítve egymáshoz ismét felvett 12 mérési adatot. Ezt az eljárást folytatva végül 120 mérési adatot kapott, melyeket a táblázat tartalmaz. (Az ellenállásokat h hosszúságú élek között mérte, az elektródák távolságát pedig l jelöli.) Látható, hogy az ellenállás a minta hosszát növelve nõ, a szélességet növelve pedig csökken.

!!\setlength!!!!\tabcolsep!!3.8pt

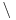h [cm] l [cm]	1	2	3	4	5	6	7	8	9	10	11	12
10	6	10	14	18	24	27	33	37	42	47	53	58
9	6	11	12	16	20	24	30	33	46	51	58	65
8	7	13	19	24	29	35	42	49	55	62	69	80
7	9	16	23	28	36	42	49	56	60	75	82	95
6	12	22	28	35	43	52	61	69	78	89	100	116
5	14	26	32	41	51	60	70	80	90	101	118	132
4	23	32	39	48	57	69	78	90	102	119	139	156
3	44	85	100	111	125	146	161	177	200	237	267	315
2	91	141	162	181	216	233	247	270	296	345	413	457
1	164	307	346	370	405	440	475	512	580	690	772	972

(A mért ellenállásértékek k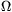-ban értendõk.)

Táblázat

Az 1. grafikonon a téglalap ellenállását ábrázoltuk az l hosszúság függvényében, néhány rögzített h szélességérték mellett, míg a 2. grafikonon rögzített hosszértékek mellett mutatja az ellenállást a szélesség reciprokának függvényében.

!!\includegraphics!!m149-1.eps

1. grafikon. Az ellenállás a hosszúság függvényében, rögzített szélesség mellett

!!\includegraphics!!m149-2.eps

2. grafikon. Az ellenállás a szélesség reciprokának függvényében, rögzített hosszúságértékek mellett

Mindkét görbesereg jó közelítéssel egyenesekbõl áll, így megállapíthatjuk, hogy az oldalak között mérhetõ ellenállás az elektródák távolságával egyenesen, a minta szélességével pedig fordítottan arányos: R=R₀^.l/h. A különbözõ méretû, de egymással geometriailag hasonló téglalapok ellenállása tehát egyenlõ, az R₀ mennyiség pedig (ami a négyzetek ellenállásának felel meg) az adott esetben kb. 50 k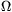-nak adódott.

• Gnadig Péter

• Megyeri Szabolcs