Geometriai optika » Fókusztávolság mérése

Jelenség leírása

Mérjük meg minél pontosabban egy kézi nagyító fókusztávolságát, s határozzuk meg a mérés hibáját is!

Eszközök

fényforrás, hosszú vonalzó, kézi nagyító

Magyarázat

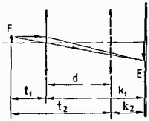
Egy gyûjtõlencse (nagyító) fókusztávolságát legközvetlenebbül úgy mérhetjük meg, hogy a lencsét párhuzamos fénynyaláb útjába állítjuk, és egy ernyõvel megkeressük a fókuszpont helyét. Az ernyõ és a lencse távolsága megadja az f fókusztávolságot. Gondot okozhat azonban a nagy pontosságú párhuzamos sugárnyaláb elõállítása, valamint a lencse vastagsága miatt a lencse helyzetének pontos meghatározása.

1. ábra

Egy kicsit áttételesebben, a Bessel-féle módszerrel sokkal pontosabban meghatározhatjuk a fókusztávolságot. Az 1. ábrán látható módon egy jól definiált, minél kisebb kiterjedésû F fényforrást (magát az izzószálat, vagy egy hátulról átvilágított rést, esetleg egy diapozitívet) képezzünk le a nagyítóval egy, a fényforrástól l távolságra elhelyezett E ernyõre. Ha az ernyõt elegendõen messze helyezzük el (l>4f), a lencse helyzetét változtatva két esetben is éles képet kapunk az ernyõn: egyszer egy kicsinyítettet, egyszer pedig egy nagyítottat. E két lencsehelyzet a fénysugarak útjának megfordíthatósága következtében szimmetrikusan helyezkedik el: az egyik esetben a t1 tárgytávolság megegyezik a másik esetben a k2 képtávolsággal, és viszont. Az l, valamint a két lencsehelyzet közötti d távolság ismeretében kiszámíthatók a tárgy- és képtávolságok:

t_1=k_2=\frac{l+d}{2},\qquad t_2=k_1=\frac{l-d}{2},

és a leképezési törvény felhasználásával a fókusztávolság:

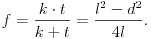
f=\frac{k\cdot t}{k+t}=\frac{l^2-d^2}{4l}.

(Látható, hogy d és l mérésének pontosságát nem befolyásolja a lencse vastagsága!)

Érdemes a mérést többször is elvégezni különbözõ l távolságok mellett, és az így kapott fókusztávolságok átlagát tekinteni mérési eredménynek, az empirikus szórást pedig eredményünk hibájának.

Az 1. táblázatban Zsigri Beáta (Szarvas, Vajda P. Gimn., I. o. t.) mérési eredményei láthatók. Az átlagos fókusztávolság:

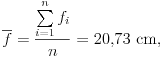
\overline{f}=\frac{\sum\limits_{i=1}^{n}f_i}{n}=20{,}73~\text{cm},

és ennek hibája:

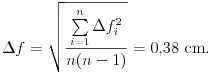
\Delta{f}=\sqrt{\frac {\sum\limits_{i=1}^{n}\Delta f^2_i}{n(n-1)}}=0{,}38~\text{cm}.

 l [cm]d [cm]f [cm]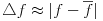\triangle f \approx|f-\overline{f}| [cm]
1.9633,521,080,35
2.861520,840,11
3.1105420,870,14
4.105,548,520,800,07
5.1024720,080,65

1. táblázat. A mérési eredmények

A mérés hibáját a nem teljesen pontszerû fényforráson és a pontatlan távolságmérésen kívül a nagyító lencsehibái is fokozhatják.

Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Zsigri Beáta
  URI STRING  
/show/645/F-I-B
  CLASS/METHOD  
show/index
  MEMORY USAGE  
613,008 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0004
Controller Execution Time ( Show / Index )  0.0092
Total Execution Time  0.0097
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0005   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('3e432c2f815f7a5e19e3e0461c9b0b30', '18.97.9.170', 'CCBot/2.0 (https://commoncrawl.org/faq/)', 1737651881) 
0.0005   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0007   SELECT *
FROM (`experiments`)
WHERE `eid` = '645' 
0.0008   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '645' 
0.0006   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '645' 
0.0003   SELECT `name`
FROM (`materials`)
WHERE `eid` = '645' 
0.0003   SELECT `source`
FROM (`sources`)
WHERE `eid` = '645' 
0.0005   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '645' 
0.0006   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '645'