Rugalmas alakváltozások » Rugalmas energia mérése

Jelenség leírása

Hajlítsunk meg egy fémfûrészlapot, illetve mûanyagvonalzót! Határozzuk meg a bennük tárolt rugalmas energiát az alakváltozás függvényében!

Eszközök

hosszú vonalzó vagy mérőszalag, rugós erőmérő

Magyarázat

A vonalzó vagy fûrészlap egyik végét rögzítsük mereven, vízszintes helyzetben, a másik végét pedig ismert nagyságú függõleges irányú F erõvel terhelve mérjük annak függõleges irányú h(F) elmozdulását az erõ függvényében (1. ábra). Ha a deformáció rugalmas, akkor az F erõ munkája megadja a meghajlított rúdban tárolt rugalmas energiát.

1. ábra

Ha a deformáció nem teljesen rugalmas, akkor ennek a munkának egy része képlékeny alakváltoztatásra fordítódik és hõvé alakul. A rugalmas energiát ekkor a meghajlított rúd kiegyenesedésekor nyert mechanikai munka adja meg. Ennek értéke szükségszerûen kisebb a meghajlításkor végzett munkánál; a két energia különbsége fordítódott képlékeny alakváltoztatásra. (Képlékeny alakváltozással csak a fûrészlap esetében kell számolnunk, a rideg mûanyag vonalzó a töréshatárig jó közelítéssel ideálisan rugalmasnak tekinthetõ.)

Az 1. táblázat, illetve az 1. grafikon Lovasi Balázs (Sümeg, Kisfaludy S. Gimn., III. o.t.) fûrészlap hajlításakor nyert adatait tartalmazza. A táblázat elsõ három sora, illetve az elsõ grafikon az erõ-lehajlás adatokat tartalmazza a deformációs, illetve a relaxációs szakaszban. Látható, hogy a két görbe nem esik teljesen egybe, a fûrészlap képlékeny alakváltozást is szenvedett. Az is látható, hogy az erõtörvény csak kezdetben lineáris. A deformációs munka az F(h) függvény numerikus integrálásával kapható meg, legegyszerûbben a trapézformula használatával:

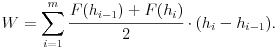
W=\sum^m_{i=1}\cfrac{F(h_{i-1})+F(h_i)}{2}\cdot(h_i-h_{i-1}).

A táblázat 4. és 5. sora tartalmazza a deformációs, ill. relaxációs szakaszban numerikus integrálással nyert munka értékeket, a 2. grafikonon pedig a rugalmas energia látható a lehajlás függvényében. Látható, hogy a képlékeny alakváltozás 6,8 mJ munkát emésztett föl.

!!\newpage!!

!!\small!! !!\setlength!!!!\tabcolsep!!0,2mm

F[N]00,10,150,20,250,30,350,40,450,50,550,60,650,70,750,8
h_\text{def}[10^{-3}\text{m}]09,51419242833374348515458626670
h_\text{rel}[10^{-3}\text{m}]10182226313540434954565963667074
W_\text{d}[\text{mJ}]00,481,041,913,044,145,767,269,8112,1913,7615,4917,9920,6923,626,7
W_\text{r}[\text{mJ}]00,40,91,62,733,835,456,69,111,512,614,316,818,821,724,8

!!\setlength!!!!\tabcolsep!!0,75mm

F0,850,90,9511,251,51,7522,252,52,7533,54
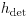h_\text{det}7477808399111123131139146152158167173
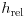h_\text{rel}78808386102113125133141148153159168174
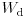W_\text{d}30,032,635,438,356,372,892,3107,3124,3140,9156,7173,9203,2225,7
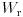W_\text{r}28,129,932,635,653,668,788,1103,2120,2136,8149,9167,2196,4218,9

1. táblázat. A fûrészlap hajlításakor nyert mérési adatok

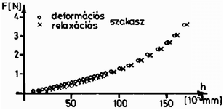
1. grafikon. A deformációs erõ a lehajlás függvényében (fûrészlap)

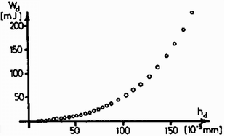
2. grafikon. A deformációs erõ munkája a lehajlás függvényében (fûrészlap)

Hasonló módon mérhetjük meg a mûanyagvonalzó deformációs energiáját a lehajlás függvényében. A 3. és 4. grafikon Páncél Csaba (Monor, József Attila Gimn., II. o.t) mérési eredményeit és a numerikus integrálással kapott energiaértékeket ábrázolja. Látható, hogy a vonalzó deformációjára a vizsgált tartományban elég jól teljesül a lineáris erõtörvény.

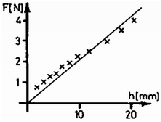
3. grafikon. A deformációs erõ a lehajlás függvényében (mûanyag vonalzó)

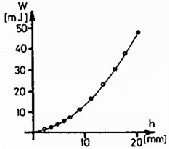
4. grafikon. A rugalmas energia a lehajlás függvényében (mûanyag vonalzó)

Kínálkozik még egy elég ötletes módszer a meghajlított rúd deformációs energiájának közvetlen mérésére. A meghajlított rúd végére helyezünk egy ismert tömegû testet, és azt ,,lõjük ki'' akár vízszintes, akár függõleges irányban. A test pályájának vizsgálatából (emelkedési magasság, repülési hossz) kiszámíthatjuk a test mozgási energiáját a kilövés pillanatában. Ha a test tömege jóval nagyobb a meghajlított rúd tömegénél, akkor a kilövéskor a meghajlított rúd saját deformációs energiájának legnagyobb részét átadja a testnek, és a deformációs energiának csak elhanyagolhatóan kicsiny része marad a kilövés után rezgõmozgást végzõ rúdban. Így alkalmas tömegû test kilövésével a pálya adataiból közvetlenül megkapható a deformációs energia. Néhányan ezzel a módszerrel végezték el a mérést.

Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Lovasi Balázs
  URI STRING  
/show/638/F-B-F
  CLASS/METHOD  
show/index
  MEMORY USAGE  
623,424 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0003
Controller Execution Time ( Show / Index )  0.0068
Total Execution Time  0.0071
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 10   
0.0003   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('a13a5aac566d1100fa997deba6d3587b', '3.144.251.72', 'claudebot', 1713303107) 
0.0008   DELETE FROM `sessions`
WHERE `last_activity` < 1713295907 
0.0005   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0006   SELECT *
FROM (`experiments`)
WHERE `eid` = '638' 
0.0006   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '638' 
0.0002   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '638' 
0.0002   SELECT `name`
FROM (`materials`)
WHERE `eid` = '638' 
0.0002   SELECT `source`
FROM (`sources`)
WHERE `eid` = '638' 
0.0004   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '638' 
0.0004   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '638'