Jelenség leírása
Vizsgáljuk meg kísérletileg, hogy mikor áll meg hamarabb az inga, ha nagyobb vagy ha kisebb méretû golyó van a fonál végén! Függ-e a megállási idõ a golyó anyagától?
Eszközök
állvány, stopper, vonalzó
Magyarázat
A mérés megkezdésekor nem gondoltam volna, hogy ennyire hosszadalmas lesz. A legnagyobb problémát az jelentette, hogy nem lehet pontosan megállapítani, mikor is áll meg az inga. Nem lehet egy adott pillanatot pontosan megjelölni, hogy igen, most már áll! Ennek ellenére megpróbáltam a ,,megállásra'' objektív kritériumot találni, s a következõ módon jártam el. A felakasztott, álló helyzetben lévõ golyó középpontjával egy vonalban egymástól kis távolságra két lapot helyeztem el úgy, hogy a golyónak éppen a felét takarják el (lásd az ábrát). Az ingát szembõl vizsgálva (onnan tudtam, hogy pont szemben vagyok a golyóval, hogy a közelebbi lap teljes egészében takarta a távolabbit), egészen pontosan meg tudtam állapítani, hogy mekkora épp a golyó kitérése. Az ábrán látható a felépítés vázlata:
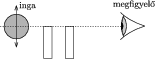
Amikor a kitérés 1 milliméter alá csökkent (ekkor szemmel már alig látható a golyó mozgása), úgy tekintettem, hogy megállt a golyó.
Magát az ingát vékony cérnából készítettem (mert kevesebb az egyenetlenség rajta, mint egy sima madzagon), és cellux segítségével a mennyezethez ragasztottam. Hosszabb ingával pontosabb mérési eredményekre számítottam. A golyó méretét úgy növeltem, hogy egyszerû játékgyurmából gyúrtam golyót, majd újabb és újabb gyurmarétegeket ,,építettem'' minden alkalommal köré. A cérna alsó végére egy csavaranyát kötöztem, és abba nyomtam bele a legelsõ gyurmát, így jobban a helyén maradt. Arra figyeltem, hogy az újabb és újabb gyurmarétegek a csavaranyától egyenlõ távolságra legyenek, s így a tömegközéppont helyzete lehetõleg a golyó közepénél maradjon.
Elkészítettem az ingát, felkötöttem a csavaranyát, belenyomtam a gyurmagolyót, majd lemértem a golyó keresztmetszetét és a tömegét. Ezután bejelöltem a papírlapon, mennyire térítettem ki az ingát, mielõtt elengedtem, hogy az összes többi lengést is ebbõl a magasságból indíthassam. Lemértem, hogy mennyi idõ alatt ,,állt meg'' az inga. Folytatva a mérést egy új réteget építettem a golyóra, újra lemértem a tömegét, átmérõjét és megállásának idejét és így tovább. Összesen 5 különbözõ méretû golyó megállási idejét mértem le. (A harmadik mérés folyamán sajnos leesett az ingám, túl gyengének bizonyult a cellux! Igazából maga a cellux fennmaradt a mennyezeten, csak a cérna csúszott ki belõle. Ennek elkerülésére a cérnát pillanatragasztó segítségével erõsítettem a celluxhoz, majd a mennyezethez. Így már elég erõs volt, azóta is ott van!)
A kapott eredményeket táblázatba foglaltam, majd grafikonon ábrázoltam a megállás idejét az átmérõ függvényében. Arra számítottam, hogy a méret növelésével (mivel a homlokfelület növekedésével nõ a légellenállás) csökkenni fog a megálláshoz szükséges idõ. Nem így lett, épp ellenkezõleg történt!
Úgy gondolom, ez amiatt van, hogy bár ugyanolyan magasról indítottam az ingákat, mégis - a nagyobb tömeg miatt - a nagyobb méretû golyók nagyobb helyzeti energiával rendelkeztek az indításkor (Eh = m g h), és hosszabb ideig tart, amíg ez a nagyobb energia apránként elvész a közegellenállás következtében. Ezt az ,,elméletemet'' további mérésekkel és számolással is próbáltam bizonyítani. Új adatokat vettem fel a táblázatomba: lemértem a golyó pályájának maximális magasságát és az elsõ lengéskor befutott körív hosszát. Ezekbõl kiszámoltam a golyó helyzeti energiáját, maximális mozgási energiáját és a közegellenállás által végzett munkát. Azt tapasztaltam, hogy a mozgási energia körülbelül egyenesen arányos a közegellenállással, tehát feltételezésem - sajnos - nem állta meg a helyét!
Ezek után a második kérdésre koncentráltam. Ugyanazt az ingát használtam, mint az elsõ részben, csak különféle anyagból készült, megközelítõleg azonos méretû golyók megállási idejét mértem. Elõször egy mûanyag golyóét, utána egy üveggolyóét, majd egy gyurmáét, amit megközelítõleg akkorára gyúrtam, mint az elsõ két golyó. A mûanyag- és az üveggolyót pillanatragasztó segítségével erõsítettem a cérnához. Azt tapasztaltam, hogy a mûanyag golyó 3 perc 24 másodperc, az üveggolyó 6 perc 9 másodperc, a gyurmagolyó pedig 4 perc 35 másodperc alatt állt meg. Tehát a feladatban feltett kérdésre a válasz az, hogy igen, függ a megállási idõ a golyó anyagától.
Szél Péter (Szekszárd, Garay J. Gimn., 12. évf.)


