Rugalmas alakváltozások » Lépcsőjáró rugó

Jelenség leírása

Mérjük meg, hogy mekkora mechanikai munkát végzünk akkor, ha egy lépcsõjáró rugót (más néven: SLINKY-rugót) lassan úgy emelünk fel, hogy csak a legfelsõ menetét fogjuk. A menetek távolságának vizsgálatával állapítsuk meg, hogy milyen magasra került a rugó tömegközéppontja!

Eszközök

állvány, lépcsőjáró (SLINKY-) rugó

Magyarázat

225 g tömegû, 90 menetes fémbõl készült lépcsõjáró rugót használtam a méréshez. A legfelsõ menetet madzaggal összekötöttem, abba akasztottam bele egy rugós erõmérõt. Folyamatosan emeltem fel az erõmérõt, és 10 centiméterenként leolvastam az erõmérõ által mutatott (l emelési magassághoz tartozó) F(l) értékeket.

A függvénykapcsolatot grafikusan ábrázoltam, ezen az általunk végzett mechanikai munka a görbe alatti területbõl olvasható le. (A grafikon legjobban egy másodfokú függvény fél-parabolájához hasonlított.) A görbe alatti területet úgy számoltam ki, hogy a mérési adatok pontjai között egyenessel közelítettem a függvényt, és az így adódó kis trapézok területét számoltam ki, majd összegeztem azokat. Az így kapott mechanikai munka 2,51 J volt.

A tömegközéppont meghatározását úgy végeztem, hogy a rugót egy állványra akasztottam, és úgy állítottam be az állvány magasságát, hogy a rugó alja még éppen a földön maradjon. 10  centiméterenként megmértem a menetek távolságát, és az egyes menetek tömegközéppontjának hi magasságát a menet aljának a földtõl mért távolságából, valamint a menettávolság felének összegébõl számítottam ki. A rugó minden egyes menetének tömege ugyanannyi: a rugó M össztömegének és a menetszámnak a hányadosa, tehát mi=2,5 g. Az egész rugó tömegközéppontjának H magassága a

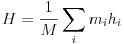
H=\frac{1}{M}\sum_{i}m_{i}h_{i}

képlet alapján számítható (lásd pl. Budó Ágoston: Kísérleti fizika I.). Az eredmény: H=58,5 cm.

Megjegyzés: A rugó emelésekor végzett munka nem egyezik meg egy M tömegû pontszerû test H magasságba emelésekor végzendõ MgH munkával, hanem annak mintegy kétszerese. A különbség onnan származik, hogy a lépcsõjáró rugónak nem csak a gravitációs helyzeti energiája növekszik, hanem rugalmas energiára is szert tesz.

Szél Péter (Szekszárd, Garay J. Gimn., 12. o.t.) dolgozata alapján

!!\small!!28 dolgozat érkezett. 6 pontot kapott Kõrösi Márton, Láng Marcell, Meszéna Balázs, Pósa László és Szél Péter, kicsit hiányos (5 pont) Borák Balázs Sándor, Hasznos László és Rárósi Dávid megoldása. Hiányos (1-4 pont) 18, nem értékelhetõ 2 dolgozat.

Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Szél Péter
  • Varga István
  URI STRING  
/show/272/F-B-F
  CLASS/METHOD  
show/index
  MEMORY USAGE  
606,336 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0004
Controller Execution Time ( Show / Index )  0.0090
Total Execution Time  0.0095
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0006   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('2552b33a07306da9c3e02a798b871042', '3.15.239.0', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1732417863) 
0.0007   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0005   SELECT *
FROM (`experiments`)
WHERE `eid` = '272' 
0.0005   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '272' 
0.0004   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '272' 
0.0005   SELECT `name`
FROM (`materials`)
WHERE `eid` = '272' 
0.0005   SELECT `source`
FROM (`sources`)
WHERE `eid` = '272' 
0.0005   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '272' 
0.0004   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '272'