Merev testek mechanikája » Lejtőn guruló golyó ferde hajítása

Jelenség leírása

Hol ér földet az asztal szélére helyezett, változtatható hajlásszögû lejtõn leguruló golyó? Két esetet vizsgáljunk meg: a) A golyó a lejtõn mindig ugyanakkora utat fut be; b) A golyó a lejtõnek mindig ugyanakkoramagasságú pontjából indul el! Mekkora szög esetén lesz a földetérés helye legmesszebb az asztaltól?

Eszközök

Állítható hajlásszögű lejtő, állvány., hosszú vonalzó vagy mérőszalag

Magyarázat

Hol ér földet az asztal szélére helyezett, változtatható hajlásszögû lejtõn leguruló golyó? Két esetet vizsgáljunk meg:

a) A golyó a lejtõn mindig ugyanakkora l utat fut be;

b) A golyó a lejtõnek mindig ugyanakkora h magasságú pontjából indul el!

Mekkora \alpha szög esetén lesz a földetérés helye legmesszebb az asztaltól?

A Budó- és Mikola-verseny kísérleti feladatai nyomán

A kísérlethez egy 8 mm átmérõjû acélgolyót használtam. A mérési elrendezés az 1. ábrán látható. A lejtõt egy L=1 m hosszú, 4 cm széles gyalult, majd polírozott falécbõl készítettem, a két oldalára vékony lécekbõl peremeket erõsítettem. A hajlásszöget úgy változtattam, hogy a lejtõt különféle méretû könyvekkel támasztottam ki, és a lejtõ végét két apró szeggel rögzítettem az asztalhoz.

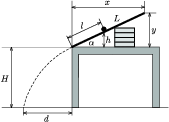
1. ábra

A hajlásszöget az x és y távolságok lemérése után az \alpha=\mathop{\rm arctg}\frac{y}{x} összefüggésbõl számítottam ki. A golyó indítási pontjaihoz tartozó l távolságokat, illetve h magasságokat mérõszalag és vonalzók segítségével határoztam meg. Az asztal magassága H=78,7 cm volt.

A golyó földetérési pontjának a lejtõ végétõl (az asztal lábától) vízszintesen mért d távolságát a következõ módon határoztam meg. Az asztal egy puha szõnyegen állt. A asztal mellé a szõnyegre A4-es lapokból összeragasztott széles papírcsíkot fektettem. A leesõ acélgolyó szabad szemmel is jól látható ,,horpadásokat'' okozott a papír felületén. Ezeket grafitceruzával bejelöltem, majd a d távolságokat minden mérési sorozat után gondosan lemértem. A golyó minden kiindulási helyzeténél 5 mérést végeztem, az eredményeket átlagoltam, a mérések hibáit a szórások alapján becsültem.

Mérési eredmények. a) Adott l (például l=30 cm) mellett azt tapasztaltam, hogy a földetérés helye és az asztal távolsága az \alpha szög maximummal rendelkezõ függvénye, legnagyobb értékét kb. 24o és 30o között veszi fel (2. ábra).

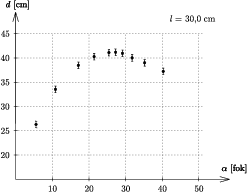
2. ábra

b) Ha a golyót a lejtõnek ugyanolyan magasságú pontjából indítjuk, pl. h=10 cm magasról, akkor is egyetlen jellegzetes maximummal rendelkezõ függvényt kapunk (3. ábra). A maximum helye 8o és 14o közé esik. Hasonló jellegû a görbe más h magasságok esetén is, de a maximum helye változhat.

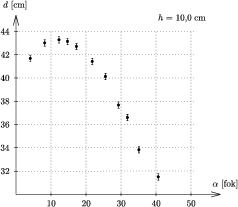
3. ábra

Az eredmények értékelése. Ha a súrlódás és a közegellenállás elhanyagolható lenne, akkor a d távolság elméletileg várt értékét a ferde hajítás képleteibõl ki tudnánk számítani. Adott h magasságból induló golyó esetén a golyó sebessége a lejtõ alján a hajlásszögtõl független lenne (energiatétel), s a d távolság az \alpha szögnek nyilvánvalóan monoton csökkenõ függvénye lenne. A kísérletben ténylegesen mért maximumgörbe ezek szerint a golyó és a lejtõ közötti súrlódás és/vagy a közegellenállás hatását tükrözi.

Láng Marcell (Budapest, ELTE Apáczai Csere J. Gyak. Gimn., 9. o.t.)

!!\small!!44 dolgozat érkezett. 6 pontot kapott Hasznos László, Kõrösi Márton, Láng Marcell, Mészáros Ágnes, Meszéna Balázs és Pósa László megoldása. Kicsit hiányos (5 pont) 9, hiányos (1-4 pont) 25, nem értékelhetõ 4 dolgozat.

Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Budó-verseny
  • Láng Marcell
  • Mikola-verseny
  URI STRING  
/show/271/F-B-E
  CLASS/METHOD  
show/index
  MEMORY USAGE  
622,184 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0005
Controller Execution Time ( Show / Index )  0.0092
Total Execution Time  0.0097
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0013   SELECT *
FROM (`sessions`)
WHERE `session_id` = '6b44428dbe69d76a47860fc2d43d2ed9'
AND `user_agent` = 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;' 
0.0006   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0006   SELECT *
FROM (`experiments`)
WHERE `eid` = '271' 
0.0005   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '271' 
0.0004   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '271' 
0.0006   SELECT `name`
FROM (`materials`)
WHERE `eid` = '271' 
0.0005   SELECT `source`
FROM (`sources`)
WHERE `eid` = '271' 
0.0006   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '271' 
0.0005   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '271'