Jelenség leírása
A legegyszerûbb fémfûrészlapok kb. 30 cm hosszúak, végeiknél kisméretû lyukak vannak. Kössük össze a lyukakat különbözõ hosszúságú, erõs zsinegekkel. Hogyan függ a fûrészlap maximális behajlása (y) a két lyuk közötti (x) távolságtól? Mérjük meg azt is, hogyan függ a zsineget feszítõ F erõ az x távolságtól!
Eszközök
fűrészlap, rugós erőmérő, vonalzó
Magyarázat
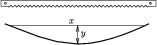
Kocsis Vilmos (Szeged, SZTE Ságvári E. Gyak. Gimn., 12. évf.) a fûrészlapot függõlegesen egy állvány talpának szélére állította, a felsõ végét pedig egy fonállal lazán az állvány függõleges rúdjához erõsítette. (A mérés során a kikötõ fonalat mindig vízszintesre állította be, így az nem fejthetett ki függõleges erõt.) A fûrészlap felsõ lyukjához fonalat erõsített, a fonalat átfûzte az alsó lyukon, majd a fonal másik végét egy súlysorozat különbözõ tagjaival terhelte. Egy - az állvány függõleges rúdjához illesztett háromszögvonalzó segítségével - megmérte x és y értékét az F terhelõerõ függvényében, majd ábrázolta az F(x) és y(x) függvényeket.
Hasonló módon járt el Meszéna Balázs (Fazekas M. Fõv. Gyak. Gimn., 11. évf.) is, de õ nehezékként vizet használt, melyet egy hitelesített ,,kupicás pohár'' segítségével kimért, fokozatosan növelt súlyú vízzel terhelte meg a fonalat. Az egységnek választott pohárnyi víz súlyát egy nagyobb, ismert méretû hengeres pohár segítségével határozta meg, és 3,3 N-nak találta.
A fûrészlap felsõ végét kézzel óvatosan úgy tartotta, hogy a függõleges fonál az alsó lyuknál lehetõleg hozzá se érjen a fûrészhez. Amikor az egyensúly beállt, egy krokodilcsipesszel rögzítette a fonalat a fûrész alsó végénél, majd a súlyt levéve kényelmesen meg tudta mérni az adott terheléshez tartozó x és y értékeket.
Terheletlen esetben a lyukak távolsága 29,5 cm volt. A terhelést fokozatosan növelve azt tapasztalta, hogy eleinte a fûrészlap nem hajlik semennyire. Kb. 10 egységnyi súlynál (3,3 N-nál) azonban ,,hirtelen'' elkezdõdik a behajlás, ez eleinte gyors ütemû, majd az egészen nagy alakváltozásnál (x<9 cm) ,,telítésbe megy'', sõt még egy kicsit csökken is (1. ábra).
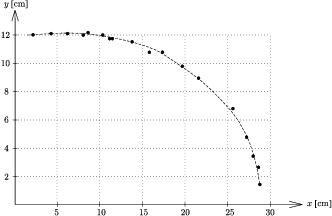
1. ábra
Hasonló módon ábrázolhatjuk a fonalat feszítõ erõt a fûrészlap lyukjai közötti x távolság függvényében (2. ábra). A mérési adatok lineáris, vagy ahhoz közeli kapcsolatot mutatnak. A nulla kihajláshoz (x=29,5 cm-hez) tartozó ,,kritikus erõ'' az egyenes extrapolált értéke alapján kb. 11 önkényes súlyegység, ami 3,6 N-nak felel meg. (Meszéna Balázs ezt a mért értéket összevetette az elméleti megfontolásokból származó elméleti képlettel, s ebbõl becslést adott a fûrészlap anyagának Young-modulusára. A kapott 300 GPa érték megegyezik a táblázatokban található adatok nagyságrendjével.)
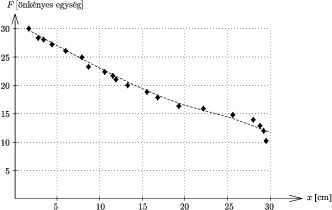
2. ábra
Többen felfigyeltek arra a jelenségre, hogy az erõsen deformált fûrészlap a zsineget feszítõ erõ csökkentésével, majd ismételt növelésével nem ugyanúgy hajlik meg, mint az elsõ alkalommal, hanem ,,emlékszik'' az elõéletére, maradandó alakváltozást szenved.
A mérés pontosságát a súlymérés és a távolságmérés hibája határozta meg, mindkettõ néhány százaléknak vehetõ. Szisztematikus hibát okozhatott a lyukon átvezetett zsineg és a fûrészlap közötti súrlódás (ezt fõleg kis súlyok esetén nehéz kiküszöbölni), valamint a fûrészlap felsõ felének rögzítésénél esetleg fellépõ függõleges irányú erõ.
!!\small!!13 dolgozat érkezett. 6 pontot kapott Kocsis Vilmos és Meszéna Balázs, 5 pontot Illés Máté, Láng Marcell, Mészáros Ágnes, Sárvári Katalin és Tüzes Dániel. Hiányos (2-4 pont) 5, mérési adatok hiányában nem értékelhetõ 1 dolgozat.


