Egyéb optika » TV képernyő (monitor) színei

Jelenség leírása

Lupén keresztül szemlélve a színes monitort, vagy a színes TV képernyõjét kék, zöld és vörös pontokat vagy szakaszokat láthatunk. Optikai méréssel határozzuk meg két azonos színû pont vagy szakasz egymástól való távolságát mindkét esetben.

Eszközök

lupe, monitor, TV-képernyő

Magyarázat

A méréshez egy sík-domború nagyítót és egy videokamerát használtam. A nagyítót a TV képernyõjéhez illesztve szabad szemmel is láthatók a csíkok, a monitornál pedig a ,,pöttyök''. Azt is lehet látni, hogy a pöttyök távolsága lényegesen kisebb, mint a csíkoké. (Ez nem csoda, hiszen a TV-tõl messzebb szoktunk ülni, mint a monitortól.)

A nagyító sík részét a képernyõhöz illesztettem, majd szorosan a lencséhez érintettem a kamera objektívjét. A nagyítás mértékét olyan nagyra állítottam, hogy a kép még ne homályosodjon el. Ezután pillanatképet készítettem, majd a felvételt ugyanakkora nagyításnál megismételtem egy vonalzó centiméter-beosztásával is.

A felvételeket visszajátszottam a TV-n, és kimerevítettem a képeket. Látszott, hogy a lencse kicsit torzít; pl. két szomszédos csík távolsága a kép szélén és a közepén különbözõ. Emiatt a képernyõ közepén látható csíkokat (pontokat) mértem, ahogy a vonalzónak is a kép közepére esõ beosztásainak távolságát vizsgáltam.

Ha a vonalzóról leolvasható nagyítás P, k pedig az egyik csík (vagy pont) és az n-edik szomszédjának távolsága, akkor két szomszédos csík (pont) távolsága: d=Pk/n.

A monitor pontábrája olyan, hogy a piros, zöld és kék pontok egy kicsiny háromszöget alkotnak. Az egyszínû pontok is háromszögrács mentén helyezkednek el, az elemi cellák egyik oldala függõleges. A rácsállandó (d) mérési adatokból számolt átlagértéke 0,31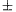\pm0,01 mm.

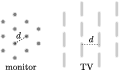
A TV képernyõjén az egyszínû függõleges csíkok egymáshoz képest vízszintesen is és függõlegesen is eltolva, vízszintesen mérve d=0,88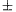\pm0,02 mm távolságban helyezkednek el. A mérés hibája a távolságmérések hibájából, a nagyító torzításából és a vonalzó beosztásának pontosságából (ez a szisztematikus hiba) adódik. Mindezeket összesítve a mérés 2-3%-ra tekinthetõ pontosnak, ez kb. egybeesik a statisztikus szórással is.

Meszéna Balázs (Fazekas M. Fõv. Gyak. Gimn., 11. o.t.)!!\\!! dolgozata alapján

Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Bakonyi Gábor
  • Meszéna Balázs
  URI STRING  
/show/265/F-I-D
  CLASS/METHOD  
show/index
  MEMORY USAGE  
605,064 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0004
Controller Execution Time ( Show / Index )  0.0101
Total Execution Time  0.0106
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0005   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('9379bb9fd1b182ff57d5a5f0c3dfec2a', '3.128.200.165', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1732411293) 
0.0009   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0006   SELECT *
FROM (`experiments`)
WHERE `eid` = '265' 
0.0007   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '265' 
0.0005   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '265' 
0.0006   SELECT `name`
FROM (`materials`)
WHERE `eid` = '265' 
0.0006   SELECT `source`
FROM (`sources`)
WHERE `eid` = '265' 
0.0007   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '265' 
0.0006   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '265'