Jelenség leírása
Öntsünk a bedugaszolt mosdóba bizonyos mennyiségû vizet. Várjuk meg, hogy a víz látszólag megnyugodjék, majd (egy lánc vagy egy madzag segítségével) hirtelen húzzuk ki a dugót! Mérjük meg a kifolyási idõt a víz mennyiségének függvényében! Törekedjünk arra, hogy örvényes és örvénymentes kifolyás is létrejöjjön!
Eszközök
hosszú vonalzó vagy mérőszalag, mosdókagyló, stopper
Magyarázat
A mérési feladat megoldása
M. 263. Öntsünk a bedugaszolt mosdóba bizonyos mennyiségû vizet. Várjuk meg, hogy a víz látszólag megnyugodjék, majd (egy lánc vagy egy madzag segítségével) hirtelen húzzuk ki a dugót! Mérjük meg a kifolyási idõt a víz mennyiségének függvényében! Törekedjünk arra, hogy örvényes és örvénymentes kifolyás is létrejöjjön!
(6 pont)
Közli: Radnai Gyula, Budapest
Megoldás. A méréseket egy kb. 40 cm oldalhosszúságú négyzet keresztmetszetû, lekerekített sarkú mosdóban végeztem. Kétféle lefolyást vizsgáltam: a nagyjából örvénymentes és az örvényes esetet. Ragasztószalagon készítettem cm-beosztást, azt ragasztottam a mosdó szélére. Ha azt az idõt mérem, amíg a víz teljesen lefolyik, akkor az utolsó centiméter nagyon pontatlanná teszi a mérést, hisz ott a víz már lassan mozog, hozzátapad a mosdó aljához, és különben sem egyértelmû, hogy mikor folyt le teljesen a víz. Ezért a ,,nullszintet'' a mosdó aljától kb. 1 cm-re vettem föl, ettõl a szinttõl mértem a vízmagasságot, és idáig mértem a kifolyási idõt. Miután feltöltöttem a mosdót a kívánt szintig, egy ideig vártam, míg a víz billegése, forgása lecsillapodik. A víz tetejére hungarocell törmeléket szórtam, és vártam, amíg a darabok mozgása megáll. (Amikor a víz látszólag már megnyugodott, a tetején úszó kis darabkák még egy ideig mozogtak; ezt a mozgást a hungarocell törmelék nélkül nem vettem volna észre.)
A dugót egy lánc segítségével húztam ki. Ha nem csináltam a vízzel semmit, akkor a kifolyás utolsó 1-2 centiméterénél csak egy nagyon vékony nyakú tölcsér jelent meg. Ha viszont a dugó kihúzása elõtt egy vonalzó segítségével megforgattam a vizet (kb. 5-6 másodperces periódusidõvel), akkor az utolsó néhány centiméteren az elõzõnél sokkal szélesebb tölcsér jelent meg. (Érdekes, hogy a tölcsér nem fokozatosan, hanem hirtelen jelenik meg.) Ez a két különbözõ lefolyás volt számomra az ,,örvénymentes'' és az ,,örvényes'' eset.
Ha a jelenséget úgy modellezzük, hogy a kifolyás során a víz billegése elhanyagolható, a lefolyó szájának mérete sokkal kisebb a mosdó méreténél, valamint a víz felgyorsulásának ideje elhanyagolhatóan kicsi, akkor érvényes a Bernoulli-törvény és a vízszint h magasságának idõbeli változására fennáll a
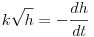
egyenlet, ahol k állandó. Innen a kezdeti H magasság és a kifolyás T ideje közötti kapcsolat:
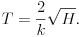
Ezen elméleti megfontolás alapján tehát azt várjuk, hogy a kifolyás ideje a kezdeti vízmagasság négyzetgyökével lesz arányos. Ez azonban csak elsõ tájékozódásnak, durva becslésnek tekinthetõ, hiszen kis kezdeti magasságnál számottevõvé válhat a folyadék felgyorsulásának ideje, a nullszint és a mosdó aljának eltérése, nagyobb vízmagasságnál pedig a billegés és a folyadék belsõ súrlódása jelentõs energiaveszteséget okozhat.
A mérések során a kezdeti vízmagasságot cm-enként változtattam 1 cm és 13 cm között. Mindegyik vízmagasságnál 3 mérést végeztem az örvénymentesnek vélt lefolyásnál, majd további 3 mérést az örvényes esetben. A mérési adatokat táblázatba foglaltam, átlagot és szórást számoltam, majd grafikusan ábrázoltam mindkét esetet (lásd az ábrát).
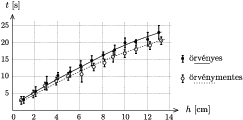
Számítógép segítségével hatványfüggvényt illesztettem a mérési adatokra. Örvénymentes esetben a legjobban illesztõ függvény (a magasságot centiméterben, az idõt másodpercben mérve):
T1(h)=2,9.h0,76,
örvényes esetben pedig
T2(h)=3,2.h0,78.
Látható, hogy a hatványkitevõ mindkét esetben nagyobb, mint amit a fent vázolt modellbõl becsültünk. Megfigyelhetõ, hogy mindegyik kezdeti magasságnál az örvényes kifolyás tartott tovább, az idõkülönbség a magassággal nõ és 12-13 cm kezdõmagasságnál eléri a 2 s-ot.
Kiváncsi voltam a ,,tölcsér'' szerepére az örvényes lefolyásnál. Vajon a lefolyás ideje azért változik meg, mert a folyadék kissé forog (és a kifolyás végén megjelenõ tölcsérnek ebben semmi szerepe nincsen, az csak ,,látvány''), vagy az idõ éppen a tölcsér miatt nõ meg? Ezek megválaszolására egy bizonyos magasságnál (13 cm-nél) alaposabban megvizsgáltam a lefolyást. Megmértem a teljes lefolyási idõt, továbbá a széles nyakú tölcsér megjelenésének elég egyértelmû pillanatát. Ezután (a mobiltelefonom stoppere segítségével) megmértem, hogy örvénymentes lefolyásnál mennyi idõ alatt folyik le a víz abból a magasságból, amelynél a másik esetben a tölcsér megjelent. Az adatokból egyértelmûen kiderült, hogy a lefolyási idõ megnövekedése csak közvetett következménye annak, hogy az elején kissé megforgattuk a vizet. A forgás miatt széles tölcsér alakul ki, és a tölcsér megjelenése miatt lelassul a kifolyás. Az elsõ 11 cm-en pl. csak 0,1 s különbséget találtam a kétféle kifolyás között (ez a mérési hibahatáron belül nullának tekinthetõ), azonban az utolsó 2 cm-en az örvényes lefolyás úgy lelassul, hogy 1,4 s-mal tovább tart, mint az örvénymentes.
Az idõmérés leolvasási hibája a reakcióidõm, kb. 0,2 s, ennél azonban szinte mindig nagyobb volt az adatok statisztikus szórása; ez utóbbi határozza meg tehát a mérés pontosságát. A hiba így 0,2-0,4 s között van.
Meszéna Balázs (Fazekas M. Fõv. Gyak. Gimn., 11. évf.)
!!\small!!20 dolgozat érkezett. 6 pontot kapott Illés Máté, Láng Marcell, Meszéna Balázs és Tüzes Dániel, 5 pontos Kocsis Vilmos, Kõrösi Márton, Mészáros Ágnes, Mirk Katinka és Szabó Áron megoldása. Kicsit hiányos (4 pont) 4, hiányos (2-3 pont) 13 dolgozat.


