Pontrendszerek » Rugalmatlan ütközés pénzérmékkel

Jelenség leírása

Határozzuk meg két egyforma pénzérme centrális, egyenes ütközésére jellemzõ ütközési számot! Végezzük el a mérést különbözõ pénzérme-párokkal!

Eszközök

pénzérmék, szögmérő, vonalzó

Magyarázat

A méréseket 1, 2, 5, 10, 20 és 100 forintosokkal is elvégeztem úgy, hogy az asztalon nyugvó egyik pénzérmének nekipöcköltem a párját. (A centrális ütközést úgy próbáltam biztosítani, hogy lazán két vonalzó közé fogtam a pénzeket, és igyekeztem olymódon meglökni az érméket, hogy a vonalzók ne akadályozzák a mozgásukat.) Az ütközés és a pénzek megállása után megmértem, hogy mennyire távolodtak el az érmék az ütközés helyétõl. Ezek az utak (s1 és s2, ahol az 1-es index a kezdetben nyugvó pénzre utal) arányosak az érmék ütközés utáni kezdõsebességének négyzetével (2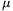\mug s=v2). Az ütközési szám definíciója: k az ütközés utáni sebességkülönbségek és az ütközés elõtti sebességkülönbségek aránya. Ezek szerint (a tömegek egyenlõségét és az impulzusmegmaradás törvényét is felhasználva):

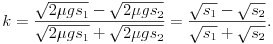
k=\frac{\sqrt{2\mu gs_{1}}-\sqrt{2\mu gs_{2}}}{\sqrt{2\mu gs_{1}}+\sqrt{2\mu gs_{2}}} =\frac{\sqrt{s_{1}}-\sqrt{s_{2}}}{\sqrt{s_{1}}+\sqrt{s_{2}}}.

Mindegyik pénzérme-párnál 10-10 mérést végeztem, ezekbõl számolt és átlagolt k-k rendre (növekvõ névértékû sorrendben): 0,71; 0,49; 0,68; 0,63; 0,56; 0,64 és 0,28. A mérési adatokból számolt k értékek szórása (az átlagtól való eltérés átlagos nagysága) 10 százalék körüli, lényegesen (mintegy 10-szer) nagyobb, mint amennyi a leolvasási pontosság alapján várható lenne. Felmerült az a gyanú, hogy az ütközési szám - a szakkönyvekben leírtakkal ellentétben - esetleg lényegesen függhet az ütközõ érmék sebességétõl; de az adatok csoportosítása (k-t ábrázoltam az ütközés erõsségére jellemzõ 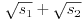\sqrt{s_{1}}+\sqrt{s_{2}} függvényében) nem erõsítette meg ezt a feltételezést. A nagy szórást tehát más hatások, feltehetõen a ,,terelõ'' vonalzókkal való ütközések okozhatták.

A mérési eredmények azt mutatják, hogy a pénzérmék kicsit különbözõ mértékben ugyan, de meglepõen ,,rugalmasak'', egyedül a 100-asok ütközése tér el a többitõl, ez a pénz - szabad szemmel is láthatóan - rugalmatlanabb a többinél.

Meszéna Balázs (Fazekas M. Fõv. Gyak. Gimn., 10. évf.)!!\\!! dolgozata alapján

Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Meszéna Balázs
  • Varga István
  URI STRING  
/show/257/F-B-D
  CLASS/METHOD  
show/index
  MEMORY USAGE  
605,744 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0003
Controller Execution Time ( Show / Index )  0.0057
Total Execution Time  0.0061
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0003   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('dbdc3ba6484c5cb2e68a1d6da004c773', '3.145.42.94', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1714107256) 
0.0004   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0007   SELECT *
FROM (`experiments`)
WHERE `eid` = '257' 
0.0005   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '257' 
0.0003   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '257' 
0.0004   SELECT `name`
FROM (`materials`)
WHERE `eid` = '257' 
0.0004   SELECT `source`
FROM (`sources`)
WHERE `eid` = '257' 
0.0003   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '257' 
0.0002   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '257'