Rugalmas alakváltozások » Torziómodulus mérése

Jelenség leírása

Torziós lengések segítségével mérjük meg egy hajszál torziós állandóját (direkciós nyomatékát)! Végezzük el a mérést különbözõ páratartalmú levegõben, és vizsgáljuk meg a lengések csillapodását is!

Eszközök

állvány, mérőszalag, stopper, vonalzó

Magyarázat

,,A mérés eléggé összetett volt, de a sok türelmet és néha agysebészi mozdulatokat igénylõ munka meghozta az eredményt; a mérési adatokból sikerült érdekes következtetéseket levonni.'' - írja Szabó Áron (Debrecen, Fazekas M. Gimn., 12. évf.). A továbbiakban is (némi rövidítéssel) az õ megoldását követjük.

1. A mérés elve. Egy függõlegesen kifeszített hajszál közepére vízszintesen egy megfaragott gyufaszálat erõsítettem, ennek a lengésidejébõl határoztam meg a hajszál (tulajdonképpen két egyformának tekintett hajszálból álló rendszer) torziós állandóját.

A harmonikus rugórezgés 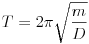T=2\pi\sqrt{\frac{m}{D}} rezgésidejének analógiájából adódik a torziós lengések periódusidejének 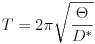T=2\pi\sqrt{\frac{\Theta}{D^*}} képlete, ahol 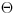\Theta ez esetben a gyufaszál tehetetlenségi nyomatéka a (tömeg)középpontján átmenõ tengelyre, D* pedig a két fél hajszál torziós állandójának az összege. Ez a rezgésidõ az amplitúdótól függetlenül állandó, még akkor is, ha a lengés csillapodik (lásd pl. Budó Á.: Kísérleti fizika, I. kötet, 88. .). Az elõzõ képlet alapján 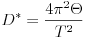D^*=\frac{4\pi^2\Theta}{T^2}. A gyufaszál (tömör, homogén, vékony rúd) 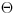\Theta-ja az adott tengelyre 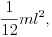\frac{1}{12}ml^2, ha m a gyufa tömege és l a hossza.

A lengés csillapodását vizsgálva azt kapjuk majd, hogy a kitérési maximumok egy exponenciális függvényre illeszkednek. A kitérés-idõ függvény alakja az elméleti várakozás (lásd pl. Budó I., ugyanott) szerint

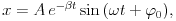
x=A\,e^{-\beta t}\sin\,(\omega t+\varphi_{0}),

ahol x a pillanatnyi kitérés, A konstans, 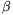\beta a csillapodási állandó (1/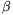\beta idõ alatt csökken a lengési amplitúdó e-ed részére), 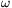\omega a körfrekvencia, 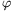\varphi0 pedig a kezdõfázis.

A feladatnak része volt a mérés elvégzése különbözõ páratartalmú légterekben. A páratartalom nyilván befolyásolja a hajszál hosszát (a hajszálas higrométerek is ezen az elven mûködnek), esetleg más tulajdonságait is, ami miatt D* változik.

2. A mérés leírása. Az eredeti gyufaszál fejét levágtam, a megmaradó rész hossza 5 cm volt. A tömegét 4 tizedesjegy pontossággal mérõ digitális mérleggel mértem és 0,0930 g-nak találtam. A gyufa közepét vonalzóval kijelöltem, és egy nagyon vékony tûvel hosszában kihasítottam (nem fúrtam lyukat). Ez csak a negyedik gyufaszálnál sikerült elfogadhatóan. A hasítás azért volt jobb, mint a lyukfúrás, mert így stabilan tudtam a hajszálat rögzíteni a gyufához. A hajszál hossza kb. 15 cm volt, amibõl függõlegesen 10,2 cm állt, a többire a rögzítéshez volt szükség.

Az asztallaphoz celluxszal kartonlapot erõsítettem, erre egy adott középpontból kiindulva 5 fokonként szögbeosztást rajzoltam. A hajszál egyik végét pillanatragasztóval a szögmérõ középpontjához ragasztottam, a másik végét átbújtattam a gyufaszálon elkészített hasítékon. (A gyufaszálon levõ rést eközben egy tûvel szét kellett feszítenem.) A hajszál szabad végét egy kör keresztmetszetû ceruzához ragasztottam, majd annyit tekertem fel a hajszálból a ceruzára, hogy a szál szabadon maradó része 10,2 cm legyen. Ez a hossz azért fontos, mert a gyufa 2 mm széles, így a hajszálból éppen a beállítani kívánt kétszer 5 cm marad szabadon. A ceruzára tekert hajat leragasztottam, majd pillanatragasztóval a gyufát is rögzítettem a hajszálhoz, méghozzá úgy, hogy kitérésmentesen éppen a 0 fokos szögbeosztásnál álljon. A hajszál kifeszítését néhány könyvre és jegyzettömbökbõl származó lapokra bíztam és úgy oldottam meg, hogy a ceruza mindkét vége alá ugyanolyan magas tornyot építettem (1. ábra). A mindkét végén rögzített és kicsit megfeszített hajszál azért elõnyös, mert ekkor a gyufaszál csak elfordulni képes, oldalirányú lengéseket nem tud végezni.

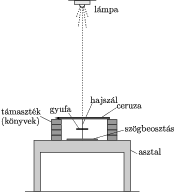
1. ábra. A mérési elrendezés vázlatos rajza

A gyufaszál elfordulásának szögét úgy mértem, hogy a szobát besötétítettem, csupán egyetlen mennyezeti lámpát hagytam égve, amely (az asztal megfelelõ eltolása után) pontosan a hajszál fölé került. A viszonylag távoli fényforrás által létrehozott árnyék körvonalai jól kivehetõk voltak, pontosan mutatták a gyufaszál eltérülését. A kezdeti szögkitérést mindig 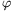\varphi0=90o-nak választottam.

A páratartalom mérésére egy régi, NDK gyártmányú hajszálas higrométert használtam, ami a levegõ relatív páratartalmát mérte. Elvégeztem a mérést száraz (43%-os páratartalmú) napon, egy másik napon 49%-os páratartalomnál, esõs idõben (63%-os páratartalomnál), végül a konyhában különbözõ mértékû gõzölés után (amikor 74%-os illetve 85%-os páratartalmat mértem).

3. Mérési eredmények. Minden páratartalom esetén 3-szor végeztem el a lengések idejének mérését. Az egyes félperiódus-idõket nem mértem, mivel az a mérési elvnél leírtak szerint nem változik, hanem 5 teljes lengés lezajlása után állítottam meg a stoppert, és a mért értéket 5-tel osztva kaptam meg a periódusidõt. Az adatokat táblázatba foglaltam, a mért idõkbõl számolt átlagokkal és szórásokkal (relatív hibákkal) együtt. A rezgés csillapodását 43%-os páratartalom mellett figyeltem; ekkor azt az idõt is megmértem, amennyi alatt a lengés gyakorlatilag teljesen megállt, továbbá megmértem az egyre csökkenõ amplitúdójú lengések legnagyobb kitéréseit, vagyis azokat a szögelfordulásokat, amelyeknél a forgás visszafordult. Eredményeimet táblázatba foglaltam és grafikonon is ábrázoltam (2. ábra).

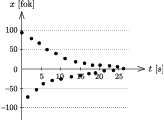
2. ábra. A szögkitérés fokokban mért maximumai az idõ függvényében

4. A mérés kiértékelése és a hibák értelmezése. A csillapodást ábrázoló grafikonon jól kivehetõ az amplitúdó exponenciális jellegû csökkenése. A szélsõ helyzetekben a szinusz függvény 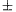\pm1 értéket vesz fel, így ilyenkor a szögkitérések abszolútértékei várhatóan egy exponenciálisan csökkenõ 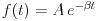f(t)=A\,e^{-\beta t} függvényre illeszkednek. Ha tehát a szögek mérõszámainak természetes (e alapú) logaritmusát képezzük és ezeket az idõ függvényében ábrázoljuk, az ln f=ln A-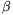\betat összfüggésnek megfelelõen egy egyenest kapunk. Ezeket a lépéseket elvégeztem, és a legjobban illeszkedõ egyenes adatainak leolvasásával ln A-ra 4,53-at, vagyis A=93-at, 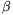\beta-ra pedig 0,128-at kaptam. Értelemszerûen A mértékegysége fok, 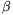\beta-é pedig 1/s.

A különbözõ páratartalmú környezetben végzett mérésekbõl kiszámított direkciós nyomatékokat a páratartalom függvényében ábrázolva megállapítható, hogy a vizsgált tartományban D* lineárisan függ a relatív páratartalomtól (p), és az adatokra legjobban illeszkedõ egyenes egyenlete:

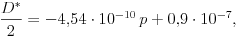
\frac{D^*}{2}=-4{,}54\cdot10^{-10}\,p+0{,}9\cdot10^{-7},

ha D*-ot Nm-ben, p-t pedig százalékban mérjük. A negatív meredekség azt a tapasztalati tényt fejezi ki, hogy a páratartalom növekedtével a hajszál torziós állandója lecsökken.

A lengések exponenciális ütemû csillapodása arra utal, hogy a fékezõerõk (közegellenállás és a hajszál belsõ súrlódása) közelítõleg a sebesség elsõ hatványával arányosak. (Ilyen elméleti feltevésbõl származtatható mozgásegyenlet megoldása valóban exponenciális csillapodást mutat.) Szükséges megjegyezni, hogy az ,,elméleti'' exponenciális görbe amplitúdója sosem csökken nullára, csak minden határon túl megközelíti azt. A valóságban azonban nagyon kis amplitúdók esetén a külsõ hatások (pl. a légáramlatok) okozta szögsebességváltozás összemérhetõvé válik a gyufa pillanatnyi szögsebességével, így a mozgás eltér az elméleti megfontolásokból kapottaktól; pl. a mérési pontosságon belül azt tapasztaljuk, hogy a gyufaszál lengése véges idõ alatt megáll.

A mérés pontosságát a fényforrás jó beállítása, valamint a gyufa és a hajszál stabil rögzítése (tehát viszonylag pontos mérési körülmények) mellett a szögmérõ beosztásának pontossága, a légáramlatok zavaró hatása és az észlelõ szemének ,,lemaradása'' korlátozza. A csillapodási adatokat tartalmazó táblázatból (illetve az ezeket ábrázoló grafikonból) megbecsülhetõ, hogy a csillapodási tényezõ mérési pontossága kb. 6-10%. A lengésidõk relatív hibájának átlaga 1,5%. A nagyobb pontosság magyarázata: itt már nem volt szükség az elfordulási szögek mérésére, hanem csak az idõtartamokéra, s ez (több lengés idejének együttes mérésével) igen pontossá tehetõ. A többi tényezõ mérési hibáját és a szisztematikus hibákat (pl. a légmozgás hatását) is tekintetbe véve a direkciós nyomaték mérési pontossága kb. 3%-osra tehetõ.

16 dolgozat érkezett. 6 pontot kapott Gálik Zsuzsanna, Mezei Márk és Szabó Áron megoldása. Kicsit hiányos (5 pont) Gyenis András, Illés Máté és Lantos Judit mérési jegyzõkönyve. 4 pontos 6, 3 pontos 3 és 2 pontos 1 dolgozat.

Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Bakonyi Gábor
  • Gálik Zsuzsanna
  • Mezei Márk
  • Szabó Áron
  URI STRING  
/show/250/F-B-F
  CLASS/METHOD  
show/index
  MEMORY USAGE  
631,672 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0003
Controller Execution Time ( Show / Index )  0.0057
Total Execution Time  0.0060
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0004   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('dd4b052f315fc869c9c4308abc491a1a', '3.141.100.120', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1713620361) 
0.0003   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0003   SELECT *
FROM (`experiments`)
WHERE `eid` = '250' 
0.0003   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '250' 
0.0004   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '250' 
0.0003   SELECT `name`
FROM (`materials`)
WHERE `eid` = '250' 
0.0003   SELECT `source`
FROM (`sources`)
WHERE `eid` = '250' 
0.0004   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '250' 
0.0004   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '250'