Jelenség leírása
Készítsünk 1,5 méter hosszú fonálingát, amelynek nehezéke egy pingponglabda! Hogyan függ a légellenállási erõ munkája (vagyis az energiaveszteség) az indítás h magasságától? Mekkora a légellenállási erõ átlagos teljesítménye egy fél lengés során?
Eszközök
fonál, hosszú vonalzó vagy mérőszalag., pingponglabda, stopper
Magyarázat
Az inga összeállítása általában nem okozott gondot a mérõk számára. A pingponglabdára a fonalat vagy cellux-szalaggal ragasztották rá, vagy pedig egy felforrósított tûvel átfúrták a labdát egyik átmérõje mentén, és a lyukon keresztül rögzítették a ,,nehezéket''. Szálként varrócérna, hímzõfonál és horgászdamil egyaránt elõfordult.
A légellenállási erõ által egy félperiódus alatt végzett munkát minden versenyzõ ugyanolyan módon, az energiacsökkenés mérésével határozta meg, az átlagteljesítményt pedig a munka és a féllengés idejének hányadosaként kapták meg. Ehhez mérni kellett az inga indítási magasságát, továbbá azt, hogy milyen magasra emelkedett az inga a túloldalon, és a közben eltelt idõt. Ezt a ,,többkezes'' feladatot már különbözõ módon oldották meg a kísérletezõk. Íme néhány ezek közül:
Szabó Áron (Debrecen, Fazekas M. Gimn., 11. évf.) szülõi segítséget vett igénybe az inga indításához, õ maga pedig az egyik kezével elkapta a túloldalon felemelkedõ labdát a pálya legmagasabb pontjánál, miközben a másik kezével a telefon stopperét használva mérte az idõt.
Vigh Máté (Pécs, PTE Babits M. Gyak. Gimn., 11. évf.) egy, az inga felfüggesztési pontjába szerelt zseblámpaizzó segítségével levetítette a labda árnyékát a talajra. A labda indításához õ is külsõ segítséghez folyamodott, de még így is megoldhatatlan kérdés maradt számára: ,,hogyan tud két ember egyszerre idõt mérni, ingát indítani és a pingponglabda árnyékát bejelölni a talajon összesen 2+2=4 kézzel?!'' Ezért videókamerával felvette az egész mérést, majd a felvételt lassítva visszajátszva határozta meg a félperiódusok idõtartamát.
Szilágyi Péter (Debreceni Egyetem Kossuth L. Gyak. Gimn., 11. évf.) egy beltéri falból kiálló kampóra szerelte az ingát, amelynek helyzetét a ,,szögmérõvé preparált'' falon követte.
Juhász Anikó (Eger, Gárdonyi G. Gimn., 12. évf.) fél centiméterenként beosztott skála segítségével határozta meg a labda indítási és felemelkedési magasságát. A lengési sík állandóságát úgy biztosította, hogy nem egyetlen szálra, hanem ,,bifilárisan'': két - egymással valamekkora szöget bezáró - fonálra függesztette fel a labdát.
Rakyta Péter (Révkomárom, Selye J. Gimn., 11. évf.) - igen ötletesen - egy segédszál segítségével úgy oldotta meg a magasságmérést, hogy az inga lengés közben valamekkora hosszban maga után húzta a szálat.
Többen észlelték, hogy viszonylag kis kitérések esetén az inga periódusideje jól egyezik egy matematikai inga lengésidejével, nagyobb kitéréseknél viszont ennél nagyobb. Szekeres Balázs (Szolnok, Verseghy F. Gimn., 12. évf.) semmit nem vett készpénznek, még a gravitációs gyorsulás értékét is megmérte. Eredménye 9,89 m/s2, és ennek a mérésnek a hibáját - nem az ,,irodalmi'' és a mért érték eltérésébõl, hanem az idõmérés és a távolságmérés pontosságából - 1 százalékosnak becsülte.
A mérési feladat jól körülhatárolt feltételei (pingponglabda, 1,5 m hosszú szál) miatt a különbözõ versenyzõk mérési eredményei jól összehasonlíthatók, hiszen a pingponglabdák tömege, mérete jó közelítéssel mindenhol ugyanakkora. Csupán a felfüggesztõ szál minõsége okozhat némi különbséget, illetve a mérés körülményei. (Többen észrevették, hogy az inga lengései igen érzékenyek a huzatra meg egyéb légáramlatokra.)
Az eredmények azt mutatják, hogy a közegellenállási erõ félperiódus alatt végzett munkája, illetve ennek átlagteljesítménye majdnem lineárisan változik az indítási magassággal. A mellékelt grafikonok Szilágyi Péter mérési adatait mutatják.
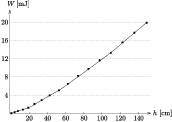
1. ábra. A légellenállási erõ munkája az indítási magasság függvényében
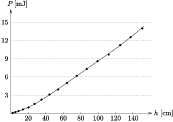
2. ábra. A légellenállási erõ átlagos teljesítménye az indítási magasság függvényében
Többen hatványfüggvény-illesztéssel megadták a W(h) és P(h) függvénykapcsolatok egyenleteit is. Íme néhány függvényalak (cm, mW és mJ egységeket használva):
W=0,04.h1,23; P=0,03.h1,19
Szabó Áron (Debrecen) mérése szerint,
W=0,037.h1,3; P=0,033.h1,28
Vigh Máté (Pécs) adatai alapján, végül
W=0,033.h1,28; P=0,037.h1,18
Szekeres Balázs (Szolnok) kísérleti eredményeit felhasználva. Látható, hogy az ország különbözõ részein különbözõ versenyzõk eltérõ eszközökkel elvégzett mérési eredményei kb. 10 százalékon belül ugyanazokat a szabályszerûségeket mutatják. Ez igen jó egyezés!


