Jelenség leírása
A bor ,,iskolázásakor'' gumicsõvel fejtik át az újbort a felsõ hordóból az alsóba. Modellezzük a folyamatot vízzel! Vizsgáljuk, hogyan függ a vízáram sebessége a szintkülönbségtõl és a csõ hosszától!
Eszközök
gumicső, mérőszalag, stopper
Magyarázat
A bor ,,iskoláztatására'' vonatkozó szakmai részleteket ábrával ellátva Csorba Emese (Hódmezõvásárhely, Bethlen G. Ref. Gimn., 10. évf.) ismerteti: ,,A nagyobb hordókból a kisebb hordókba fejtik át a bort. Mindig teli hordónak kell lenni, hogy a bor ne pimpósodjon meg. A nagyobb hordókat úgynevezett ászokra teszik. A gumicsõ vége nem érhet le a felsõ hordó aljára, mert az üledéket (az ún. seprõt) is felkavarná.''
1. ábra. A ,,mérési elrendezés'' vázlata
Komjáthy Júlia (Szekszárd, Garay J. Gimn., 12. évf.) a mérés elvégzése elõtt a lehetõ legavatottabb szakemberhez, a borász nagypapához fordult ,,az e téren lévõ tapasztalatai'' végett. A nagypapa jóslata szerint ,,a kifolyó bor sebessége nem nagyon függ a csõ hosszától; viszont minél nagyobb a szintkülönbség, annál gyorsabban folyik a bor, ... és annak, hogy a teli hordóba milyen mélyre nyomjuk le a csövet, nincs jelentõsége''. Az utóbbi két jóslat igaznak bizonyult, a csõ hosszától viszont (a súrlódások, örvények és egyéb lassító tényezõk miatt) igenis függ a sebesség, - írja saját megfigyelései alapján a versenyzõ, és ez derült ki a többi dolgozatból is. (A szakember védelmében mag kell említeni, hogy az áramlási veszteségeket a fizikus is csak viszonylag hosszú, vékony csõvel veszi észre, a borászt pedig semmi nem készteti ilyen csõ használatára. - A szerk.)
No, de lássuk a mérést! A bort a diákok természetesen vízzel helyettesítették, a hordókat pedig vödrökkel, meg mindenféle konyhai edényekkel. Szilágyi Péter (Debreceni Egyetem Kossuth L. Gyak. Gimn., 11. évf.) egy 50 literes mûanyag hordót helyezett el a tetõtérben, innen ,,iskolázta'' át a vizet a pincéig vezetõ csigalépcsõ különbözõ magasságban levõ fokaira. Õ is - mint a mérést elvégzõk többsége - a víz áramlási átlagsebességét (v) a hozamból számította ki, mérve azt az idõt, ami alatt egy másfél literes mûanyag flakon megtelik a csövön keresztül. Mérése közben a felsõ vízszint (mivel kellõen nagy hordót használt) nem változott számottevõen. Másoknak, akik kisebb edényt alkalmaztak, állandó pótlással gondoskodniuk kellett a felsõ vízszint állandóságáról. Tóth Sándor (Csongrád, Batsányi J. Gimn., 12. évf.) például vízcsapból állandóan pótolta a lefolyt vizet, sõt, még egy túlfolyót is alkalmazott a vízszint stabilitására.
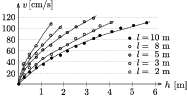
2. ábra. A vízáram sebessége a szintkülönbség függvényében
Szilágyi Péter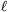 
=10, 8, 5, 3 és 2 m hosszú csövekkel végigmérte a csigalépcsõ által biztosított szintkülönbségek teljes tartományát. Ezek szerint adott csõhossz esetén az áramlási sebesség a h szintkülönbség négyzetgyökével arányosnak tekinthetõ (2. ábra), hasonlóan a szabadesés 
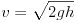összefüggéséhez. Az arányossági tényezõ a vízáramlásnál (feltehetõen a folyadék belsõ súrlódása és a csõ falával való súrlódása miatt) sokkal kisebb, néhol csak tizede, mint a szabadon esõ testek esetében. Adott szintkülönbség mellett a hosszabb csövön kisebb a vízáramlás sebessége (3. ábra), de a függvénykapcsolat határozottan nem lineáris. Számítógépes hatványfüggvény-illesztéssel v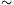
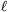-0,7 összefüggés kapható. A hatványkitevõ ,,kézzel'' (pontosabban egy zsebszámológéppel) is meghatározható, ha lg v-t lg 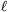függvényében ábrázoljuk, majd a mérési pontokra ,,szemmel'' (és egy vonalzóval) egyenest illesztünk.
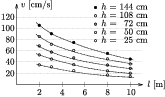
3. ábra. A vízáram sebessége a csõ hosszának függvényében
A folyadékok áramlását tárgyaló könyvek (pl. Budó Á.: Mechanika) szerint csövekben az áramlás kis sebességek esetén réteges (lamináris), nagyobb sebességeknél pedig turbulens (gomolygó, örvénylõ). A kétféle áramlás közötti átmenet - Reynolds (1883) és mások mérései szerint - akkor következik be, ha a folyadék v sebességébõl,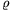 
sûrûségébõl, 
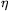viszkozitásából és a csõ r sugarából képezhetõ dimenziótlan R=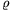r v/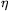 szám (az ún. Reynolds-szám) kb. 1160-nál nagyobb. Tóth Sándor megpróbálta mindkét áramlást megvalósítani, és a lamináris 
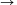turbulens átmenetet kimutatni. Azt tapasztalta, hogy kisebb sebességû áramlás más függvénykapcsolattal jellemezhetõ, mint a nagyobb sebességû, de az átmenet nem éles. A mérési adatok alapján inkább csak sejthetõ, mint bizonyítható, hogy R
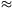1000 környékén egy kicsit megváltozik a v(h) függvény jellege. Megfigyelte azt is, hogy a mérés során apró légbuborékok jelentek meg a csõ falán, s ez csökkentette a kiömlés sebességét. Vigh Máté (Pécs, PTE Babits M. Gyak. Gimn., 11. évf.) ugyancsak megfigyelte a v(h) függvénykapcsolat jellegének megváltozását R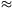1200-as Reynolds-szám környékén, ezen kritikus érték alatt lineárisnak tekinthetõ a függvény, felette pedig a négyzetgyököshöz közeli (v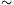h0,54).
Említést érdemel Varga Lajos (Gyula, Karácsonyi János Kat. Gimn., 10. évf.) sebességmérési módszere. Egy nyakláncból származó színes gyöngyszemet, melynek átmérõje kb. fele volt a csõ átmérõjének, sûrûsége pedig kisebb, mint a vízé, a cérnafelfûzõ lyukba tömködött gyurmadarabkákkal addig ,,nehezített'', míg a gyöngy éppen lebegett a vízben. Így a gyöngy igen könnyen, szinte ,,akadálytalanul'' együtt mozgott a vízzel, s mivel helyzete jól megfigyelhetõ, a sebességét könnyen meg lehetett határozni.
A mérés pontosságát az idõmérés hibája (néhány tizedmásodperc), a térfogatmérés hibája (néhány ml), a csõ hosszának mérésénél elõforduló hiba (cm nagyságrendû) és a külsõ körülmények esetleges változásából adódó véletlenszerû hatások korlátozzák. Mindezek, valamint az említett szisztematikus hibaforrások (pl. buborékképzõdés, a csõ hajlatainak szerepe stb.) miatt a mérés pontosságát kb. 4-5%-osnak becsülhetjük. Az adatfeldolgozás során kapott mennyiségeknek (pl. az illesztett hatványfüggény kitevõjének) a bizonytalansága is ilyen nagyságrendû.
