Jelenség leírása
Vegyünk egy végig egyforma szemekbõl álló láncot! (Lehet olyan is, amivel nemrég a karácsonyfát díszítettük.) Határozzuk meg a lánc és egy asztal felülete között a) a tapadási- b) a csúszási súrlódási együttható értékét!
Összeállítás
A mérésekben a következõ ,,láncféleségek'' fordultak elõ: nyaklánc, óralánc, különbözõ gyöngysorok, karácsonyfadíszek, kerékpárlánc, kutyalánc, bikalánc, vontatólánc stb. Néhányan többféle lánccal és többféle felületen (sõt, a mérési eredmények hitelességének ellenõrzésére többféle módszerrel) is elvégezték a mérést.
Eszközök
Állítható hajlásszögű lejtő (szögmérővel), lánc, rugós erőmérő
Magyarázat
A mérésekben a következõ ,,láncféleségek'' fordultak elõ: nyaklánc, óralánc, különbözõ gyöngysorok, karácsonyfadíszek, kerékpárlánc, kutyalánc, bikalánc, vontatólánc stb. Néhányan többféle lánccal és többféle felületen (sõt, a mérési eredmények hitelességének ellenõrzésére többféle módszerrel) is elvégezték a mérést.
A mérési módszerek is sokfélék voltak. Aszerint, hogy milyen helyzetû felületen mozgott a lánc, a módszerek 2+1 csoportba sorolhatók: egyesek vízszintes felületen, mások lejtõn mozgó láncot vizsgáltak. A +1 módszer csak egyetlen versenyzõ mérésére vonatkozik, de érdemes lesz ezt is megismerni.
A versenyzõk többsége vízszintes felületen mozgatta a láncot, vagy gyöngysort. A tapadási súrlódás mérésénél sokan azt vizsgálták, hogy az asztal szélérõl részben lelógó lánc milyen helyzetben kezd el csúszni. A lelógó és az asztalon levõ lánchosszak (láncszemszámok) arányából kapták meg a tapadási súrlódás együtthatóját. Többen észrevették, hogy ennél a módszernél elég nagy szisztematikus hibát okoz a láncszemek megakadása az asztal szélén. Geresdi Attila (Pécs, Árpád Fejedelem Gimn., 12. o.t.) arra a következtetésre jutott, hogy az ilyen módszerrel mért tapadási együttható értéke (0,45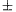 0,01) lényegesen nagyobb, mint ugyanannak a láncnak ugyanazon a felületen más módszerrel mért súrlódási együtthatója (0,27
0,01) lényegesen nagyobb, mint ugyanannak a láncnak ugyanazon a felületen más módszerrel mért súrlódási együtthatója (0,27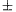 0,04). Ezen szisztematikus hiba csökkentése érdekében egyesek csigát vagy rudat szereltek az asztal szélére, és azon vetették át a láncot.
0,04). Ezen szisztematikus hiba csökkentése érdekében egyesek csigát vagy rudat szereltek az asztal szélére, és azon vetették át a láncot.
Mindkét fajta súrlódási együttható mérésénél többen alkalmazták azt a módszert, hogy az egész láncot húzták vízszintes felületen, és közben mérték a lánc elmozdításához, illetve egyenletes (vagy gyorsuló) mozgatásához szükséges erõt. Ehhez a lánc tömegétõl függõen különbözõ méréshatárú és érzékenységû rugós erõmérõket alkalmaztak, illetve valamilyen ismert (és változtatható) tömegû nehezéket használtak. Biró István (Marosvásárhely, Bolyai F. Líceum 11. o.t.) pl. homokot szórt egy kis serpenyõbe, amely egy csigán átvetett cérna segítségével mozgatta a láncot. Vigh Máté (Pécs, Babits M. Gimn., 10. o.t.) egy olyan rugós erõmérõt használt, amely közvetlenül a maximális erõt mérte, ugyanis a rugó megakadt a legnagyobb kitérésnél, s így kellõ pontossággal jelezte a lánc megmozdításához szükséges erõt. Ugyancsak õ a láncot egy játékautóból kiszerelt villanymotorral mozgatta, mert - érvelése szerint - a sebesség állandóságát akár ,,szemre'' is meg lehet állapítani, de pontosabb, ha egy kis villanymotor segítségével oldjuk meg a lánc vontatását.
A másik - ugyancsak többek által alkalmazott - módszer a lánc lejtõn való csúsztatása volt. Ennél a módszernél a lejtõ hajlásszögét változtathatjuk, s mérhetjük, hogy mekkora hajlásszög esetén csúszik meg a lánc, illetve mekkora szög esetén csúszik egyenletesen vagy gyorsulva. Szilágyi Péter (Debreceni Egyetem Kossuth L. Gyak. Gimn., 10. o.t.) mérési jegyzõkönyve szerint a lánc elhelyezése a lejtõn némi gondot okozott. Ha vízszintesen helyezte el a láncot, az gurulni kezdett; ha kupacba tömörítette, akkor a különbözõ láncszemek másképpen mozogtak; a lejtõ mentén lerakott lánc szemei pedig helyenként egymásba csúsztak. (Tapasztalata szerint még a ,,hosszanti'' láncfektetés bizonyult a leghasználhatóbbnak.)
Geresdi Attila egy harmadik - mások által nem alkalmazott - módszert is talált a tapadási súrlódási együttható mérésére. Azt vizsgálta, hogy mekkora F erõvel lehet az egyik végénél fogva egyensúlyban tartani egy rögzített hengerre felcsévélt láncot, ha a lánc másik végét F0 nagyságú erõ feszíti. Elméleti megfontolások szerint az egyensúly feltétele:
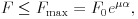
illetve
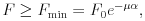
ahol  a láncnak a hengerrel érintkezõ részét jellemzõ szög (radiánban),
a láncnak a hengerrel érintkezõ részét jellemzõ szög (radiánban), 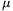 pedig a tapadási együttható. Az idézett képletek abban a közelítésben érvényesek, ha a lánc súlya a láncot feszítõ erõkhöz képest elhanyagolható; ennek biztosítása érdekében egy igen könnyû (4 g tömegû) láncot választott, amelyet az egyik végén 50 g-os súllyal terhelt. Fahenger gyanánt az iskolai szertárban talált, 3 különbözõ átmérõjû hengerbõl álló lakkozott facsigát használt, melynek középsõ, 3 cm széles tartománya alkalmas volt a méréshez. A lánc feltekerésének szögét
pedig a tapadási együttható. Az idézett képletek abban a közelítésben érvényesek, ha a lánc súlya a láncot feszítõ erõkhöz képest elhanyagolható; ennek biztosítása érdekében egy igen könnyû (4 g tömegû) láncot választott, amelyet az egyik végén 50 g-os súllyal terhelt. Fahenger gyanánt az iskolai szertárban talált, 3 különbözõ átmérõjû hengerbõl álló lakkozott facsigát használt, melynek középsõ, 3 cm széles tartománya alkalmas volt a méréshez. A lánc feltekerésének szögét 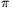 /4 és 4
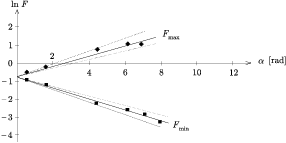
/4 és 4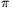 értékek között változtatva rugós erõmérõvel megmérte Fmax és Fmin értékeit (az egyik a súly felhúzásának, a másik a leengedésének határesetéhez tartozó erõ), majd ezek természetes alapú logaritmusát ábrázolta
értékek között változtatva rugós erõmérõvel megmérte Fmax és Fmin értékeit (az egyik a súly felhúzásának, a másik a leengedésének határesetéhez tartozó erõ), majd ezek természetes alapú logaritmusát ábrázolta  függvényében. A mérési adatokra egy-egy egyenest illesztett (lásd az ábrát), és ezek meredekségébõl leolvasta a tapadási súrlódási együttható mért értékét, valamint (a pontozott vonalak meredekségébõl) a mérés becsült hibáját. Így kapta a korábban már idézett
függvényében. A mérési adatokra egy-egy egyenest illesztett (lásd az ábrát), és ezek meredekségébõl leolvasta a tapadási súrlódási együttható mért értékét, valamint (a pontozott vonalak meredekségébõl) a mérés becsült hibáját. Így kapta a korábban már idézett 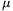 t=0,27
t=0,27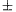 0,04 eredményt.
0,04 eredményt.
A mérési eredmények nehezen lennének összehasonlíthatók, hiszen a legkülönbözõbb felületeken és igen különbözõ láncokkal mértek a versenyzõk. Valamennyien arra következtettek, hogy a tapadási együttható nagyobb, mint a csúszási súrlódásé, de a két érték különbsége nem jelentõs, néhol alig nagyobb, mint a mérési hiba. Néhány tipikus tekinthetõ eredmény Biró István méréseibõl (az elsõ szám a csúszási, a második a tapadási együttható):
| - gyöngy festett lemezen: | 0,20 | 0,26 |
| - gyöngy fémen: | 0,28 | 0,31 |
| - gyöngy csiszolópapíron: | 0,66 | 0,89 |
| - kutyalánc festett lemezen: | 0,20 | 0,26 |
| - kutyalánc fémen: | 0,23 | 0,26 |
A mérés hibáját elsõsorban az erõmérés pontossága, illetve a lejtõs módszernél a szögmérés hibája határozza meg. Statisztikus hiba a különbözõ körülmények, illetve különbözõ módszerekkel mért adatok szórásából becsülhetõ. Reálisnak tekinthetõ a 3-5%-os relatív hiba (erõmérõ használata esetén), illetve 2-3%-os relatív hiba (lejtõs módszernél).
Megjegyzés. A versenyzõk többsége a fentiekhez hasonló mérési eredményeket és hibaszázalékokat kapott. Ettõl lényegesen eltérõ számokat csak egyetlen tanuló adott meg, õ a súrlódási együtthatókra

értékeket mért. Lehetséges, hogy a láncának ,,kereke'' volt?
!!\small!!25 dolgozat érkezett. Helyes Biró István, Geresdi Attila, Mózer Tamás, Orosz Gergõ, Szilágyi Péter, Vigh Máté megoldása. Kicsit hiányos (5 pont) Coc Károly és Tóth Sándor mérése, hiányos (1-4 pont) 17 dolgozat.


