Tömegpont dinamikája » Ferde hajítás

Jelenség leírása

Készítsünk rajztáblából egy változtatható hajlásszögû lejtõt! Illesszük a rajztábla alját az asztal széléhez úgy, hogy a lejtõn lecsúszó test ütközés nélkül hagyja el a lejtõt és essen a talajra. Mérjük meg, hogy mekkora hajlásszög esetén esik le legtávolabbra a rajztábla tetejérõl lecsúszó pénzérme! Függ-e az eredmény a rajztábla hosszától, illetve az asztal magasságától, valamint a pénzérmétõl?

Összeállítás

A mérés elvégzésekor a legnagyobb problémát az érme talajra érési helyének meghatározása okozta, mert az érme innen rendszerint továbbgurult (-repült, -pattant). A feladat megoldói a legkülönbözõbb ,,trükköket'' alkalmazták. Nagyon sokan másolópapírt helyeztek a földre, amelyen a leesõ érme jól megfigyelhetõ nyomot hagyott. Többen apró szemû anyagot (lisztet, búzadarát, homokot, teafüvet stb.) szórtak a földre, és ezt használták nyomjelzõként. Rajztábla helyett néhányan más ,,csúszó-alkalmatosságot'' (gyúródeszkát, polclapot, mérnöki rajzasztalt, plexilapot) használtak; ez a mérés lényegét nem változtatja meg, tehát elfogadható módosítás.

Eszközök

Állítható hajlásszögű lejtő

Magyarázat

A mérést elvégzõk azt az eredményt kapták, hogy a különbözõ érmék a 45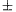\pm10 fokos szögtartomány valamelyik értéke esetén esnek legmesszebbre az asztal szélétõl. Az 1. ábrán látható grafikon Tóth Sándor (Csongrád, Batsányi J. Gimn., 11. o.t.) mérési adatait alapján készült, a becsült mérési hibákat és az adatokra ,,szemmel'' illesztett görbét is feltüntetve.

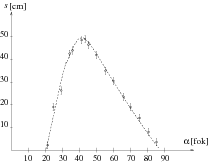
1. ábra. Az esés távolsága a lejtõ hajlásszögének függvényében

A feladat második részét nagyon sokan félreértették, és azt vizsgálták, hogy a földetérés távolsága hogyan változik a rajztábla hosszának és az asztal magasságának függvényében. A feladat az elsõ részfeladat mérési adataiból kiolvasható eredménynek, vagyis annak a szögnek a fentiektõl való függését kérdezte, amelynél az érme a legtávolabbra esik. Ezt a részfeladatot csak néhányan oldották meg elfogadhatóan; õk azt kapták, hogy az ,,optimális szög'' a mérési hibahatáron belül nem függ sem a pénzérmétõl (annak ,,névértékétõl''), sem pedig az asztal magasságától. A rajztábla hosszával kapcsolatban megoszlottak a vélemények. Geresdi Attila (Pécs, Árpád Fejedelem Gimn., 12. o.t.) és Orosz Gergõ (Miskolc, Földes F. Gimn., 12. o.t.) nem tudtak kimutatni a mérési hibán belül ilyen függést. Kiss Imre (Pécs, Babits M. Gyak. Gimn., 10. o.t.) és Tóth Sándor viszont azt találta, hogy ez a szögérték (amelynél a legmesszebbre repül az érme) enyhe csökkenést mutat az indítási magasság növelésekor. A 2. ábrán látható grafikon Kiss Imre mérési adatait mutatja.

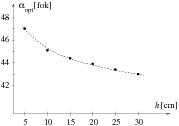
2. ábra. Az ,,optimális'' szög függése a lejtõ magasságától

A szög-, illetve helymeghatározás becsült mérési hibái 5 és 10 százalék közé tehetõk.

Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Geresdi Attila
  • Kiss Imre
  • Orosz Gergõ
  • Tóth Sándor
  URI STRING  
/show/226/F-B-C
  CLASS/METHOD  
show/index
  MEMORY USAGE  
606,640 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0004
Controller Execution Time ( Show / Index )  0.0095
Total Execution Time  0.0100
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0014   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('74b95e378fd83e6076ce0898b3b5699a', '3.147.68.201', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1732411822) 
0.0006   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0005   SELECT *
FROM (`experiments`)
WHERE `eid` = '226' 
0.0006   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '226' 
0.0003   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '226' 
0.0004   SELECT `name`
FROM (`materials`)
WHERE `eid` = '226' 
0.0004   SELECT `source`
FROM (`sources`)
WHERE `eid` = '226' 
0.0005   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '226' 
0.0005   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '226'