Merev testek mechanikája » Jégkorong visszapattanása a palánkról

Jelenség leírása

A palánkról visszapattanó jégkorong visszaverõdési szöge általában nem egyezik meg a beesési szöggel. (A jégkorong mozgását modellezhetjük falról visszapattanó befõttesüveg-tetõ mozgásával.) Hogyan függ a visszaverõdés szöge a falhoz csapódó korong (tetõ) sebességétõl és a beesési szögtõl?

Összeállítás

A mérés gondos elvégzéséhez olyan ,,korongkilövõ szerkezetre'' volt szükség, amellyel többször is (a mérési hibán belül) ugyanakkora kezdõsebességgel lehetett indítani a korongot.

Magyarázat

A mérés gondos elvégzéséhez olyan ,,korongkilövõ szerkezetre'' volt szükség, amellyel többször is (a mérési hibán belül) ugyanakkora kezdõsebességgel lehetett indítani a korongot. Ezt a technikai feladatot legtöbben valamilyen rugós vagy gumis ,,parittyával'' oldották meg. Biró István (Marosvásárhely, Bolyai Farkas Líceum 10. o.t.) ügyes szerkezetet konstruált, amely a kilövés körülményeinek reprodukálhatósága mellett a korong pályájának kirajzolását is megoldotta (1. ábra). A korong közepébe lyukat fúrt, melybe egy cérnával körbetekert fogpiszkálót helyezett. A cérnaszálat tintával itatta át, így a sima üveglapot éppen érintõ tintás cérnaszálvég kirajzolta a korong tömegközéppontjának pályáját.

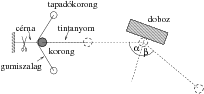
1. ábra

Ketten - Nagy Ádám (Budapest, Szent István Gimn., 12. o.t.) és Biró István - észrevették, hogy a visszapattanó korong pályája nem egyenes, hanem ,,elferdül'', ezt a megfigyelést azonban a visszapattanási szög megállapításakor nem használták ki. Valamennyi versenyzõ a már megállt korong helyzetébõl számította ki a 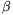\beta2 visszaverõdési szöget, ez azonban egy kicsit eltér az ütközésre jobban jellemzõ, jóllehet nehezebben mérhetõ 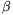\beta1 szögtõl (2. ábra).

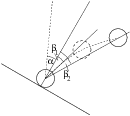
2. ábra

A mérés kivitelezésének egyik lényeges pontja a megfelelõ csúszófelület kiválasztása. Legtöbben valamilyen sima felületet választottak, amelyen a sebesség mérésénél figyelembe kellett venniük a súrlódást is. Jurányi Zsófia (Pécs, !!\hbox!!Leöwey Klára Gimn. 12. o.t.) étolajjal bekent bútorlapon végezte méréseit. Állítása szerint ezen a lapon a súrlódás elhanyagolhatóan kicsi. Geresdi Attila (Pécs, Árpád Fejedelem Gimn. 11. o.t.) egy 1 m2-es felületû légpárnás asztalon kísérletezett. A szögek mérését általában vonalzó és szögmérõ segítségével oldották meg a versenyzõk, de más megoldás is elõfordult: Sükösd Zsuzsanna (Budapest, Orsolya Rendi Szent Angéla Gimn. és Ált. Isk. 7. o.t.) például a ,,kockás'' konyhakövezet koordináta-rendszerét használta fel a korong helyének és mozgásának meghatározására.

Csaknem minden versenyzõ azt az eredményt kapta, hogy a visszaverõdési szög nagyobb, mint a beesési szög, az eltérés azonban kicsi, illetve a merõlegeshez közeli értékeknél egyre kisebbé válik. Ezt szemlélteti Szilágyi Péter (Debrecen, Kossuth L. Gyak. Gimn. 9. o.t.) 3 különbözõ sebességre utaló mérési eredményeinek grafikus ábrázolása (3. ábra). Nagy Ádám a visszaverõdési és a beesési szög arányát ábrázolta a beesési szög függvényében (4. ábra).

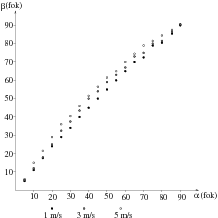
3. ábra

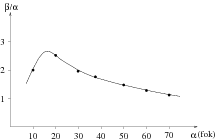
4. ábra

A szögek mérésénél nehezebb a sebességfüggés kísérleti vizsgálata. Különbözõ magasságú lejtõkrõl indított korongok sebessége közötti eltérés nem olyan nagy, hogy - a számottevõ mérési hibák mellett - egyértelmû kapcsolatot lehetne találni a szögek és a sebességek között. (Parittyás kilövõszerkezetnél az ütközés sebessége nagyobb lehet, viszont a sebesség mérése válik bizonytalanabbá.) Az 5. ábra Jurányi Zsófia mérési adatait mutatja. A 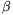\beta visszaverõdési szöget ábrázolta (a mérési pontosságot is feltüntetve a rajzon) különbözõ v ütközési sebességek esetén, a beesési szög \alpha=45o rögzített értéke mellett. 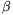Látható, hogy a vizsgált tartományban (az adott mérési pontosság mellett) \beta nem függ v-tõl.

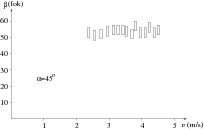
5. ábra

Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Biró István
  • Geresdi Attila
  • Jurányi Zsófia
  • Szilágyi Péter
  URI STRING  
/show/222/F-B-E
  CLASS/METHOD  
show/index
  MEMORY USAGE  
619,264 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0006
Controller Execution Time ( Show / Index )  0.0118
Total Execution Time  0.0124
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0006   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('de79c54acec0ae157637c84bc473b4ae', '18.218.38.125', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1714174287) 
0.0007   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0009   SELECT *
FROM (`experiments`)
WHERE `eid` = '222' 
0.0014   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '222' 
0.0006   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '222' 
0.0006   SELECT `name`
FROM (`materials`)
WHERE `eid` = '222' 
0.0008   SELECT `source`
FROM (`sources`)
WHERE `eid` = '222' 
0.0010   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '222' 
0.0006   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '222'