Jelenség leírása
Készítsünk mágneses ingát! Két mágneskorong egyikét rögzítsük az asztalon, a másikat függesszük fel felette úgy, hogy egyensúlyi helyzetben elég közel legyenek egymáshoz, vonzó helyzetben. Mérjük meg a kitérített ingára ható vonzóerõt a kitérítési szög függvényében!
Eszközök
kisméretű ingatest, mágnesek, szögmérő, vonalzó
Magyarázat
A legtöbben úgy végezték el a mérést, hogy az ingaszerûen felfüggesztett mágnest oldal irányú (vízszintes vagy ferde) erõvel kitérítették, és meghatározták az erõ nagysága és a kitérítés szöge közötti összefüggést. Jurányi Zsófia (Pécs, Leöwey K. Gimn., 12. o.t.) rugós erõmérõt használt (1. ábra), és ehhez kellõen erõs - kerékpárdinamóból kiszerelt - mágneseket választott. A mágneses vonzóerõ rohamos csökkenése miatt csak nagyon kis szögtartományban tudott mérni. Igen nehezen sikerült beállítania az egyensúlyi helyzetet, mert a mágnesek könnyen ,,összerántották egymást''. A mágnesek között ható vonzóerõt az erõmérõ által mutatott értékbõl és a felfüggesztett mágnes elõzõleg megmért súlyából számította ki. Mérési adatait a 2. ábra grafikonja mutatja. Látható, hogy az erõ a kitérítés szögének (a mágnesek távolságának) növekedtével rohamosan csökken.
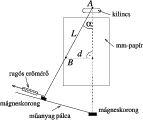
1. ábra
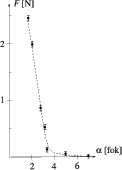
2. ábra
Nagy Ádám (Budapest, Szent István Gimn., 12. o.t.) csigán átvetett fonállal és egy súllyal vízszintes irányban húzta el a felfüggesztett mágnest (3. ábra). Csak kis kitéréseket hozott létre, így a LEGO-ból épített csigatartó torony magasságát nem kellett változtatnia. Az eltérítõ erõt mindvégig vízszintesnek tekinthette, a mágnesek között ható erõt pedig a súlyokból számítással határozta meg. (A csigánál fellépõ súrlódást nem vette figyelembe, ez szisztematikus hibát okozhatott.) Hasonló elrendezést alkalmazott Bíró István (Marosvásárhely, Bolyai F. Líceum 10. o.t.) is, de õ a szögmérés pontosságát egy ,,lézerceruza'' segítségével próbálta javítani.
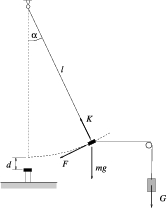
3. ábra
A sztatikus (egyensúlyi elrendezésen alapuló) mérések mellett más módszerrel is próbálkoztak a versenyzõk. Pethõ Balázs (Pécs, Babits M. Gyak. Gimn., 12. o.t.) kúpingát készített, tehát olyan mozgásba hozta a felfüggesztett mágnest, hogy annak fonala a függõlegessel közel állandó szöget zárjon be. Megmérte a kúpinga keringési idejét a kitérés szögének függvényében, majd (a mozgásegyenlet segítségével) kiszámította a két mágnes között ható erõt. A periódusidõ pontosabb mérése végett a mozgó mágnest egy lámpával megvilágította, és az árnyékot egy papírlapon figyelte meg (4. ábra). Ez a mérési módszer sem volt problémamentes, mert a mozgó mágnes síkja billegett, és a pálya sem mindig ,,sikerült'' kör alakúra.
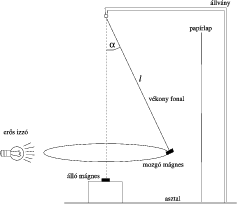
4. ábra
Szatmári Emõke (Marosvásárhely, Bolyai F. Líceum 12. o.t.) felfigyelt arra, hogy két mágnes általában nem csupán erõt fejt ki egymásra, hanem forgatónyomatékot is. (Ennek olyan következménye is van, hogy a mágnesek közötti erõ ,,nem centrális'', tehát általában nem esik egybe a mágnesek közepét összekötõ egyenessel!) A mágneseket egy-egy kifúrt és tengelyezett mûanyagvonalzóhoz erõsítette, az így készített ,,mérleget'' rézdrót súlyokkal kiegyensúlyozva próbált következtetni a mágnesek közötti forgatónyomatékra és az erõkre.
A mérési feladat meglehetõsen nehéz volt. A mágnesek beszerzése, felfüggesztése, a finom erõmérés megoldása, a mágnesek elfordulásának megakadályozása mindenkinek gondot okozott. Ez a mérés pontosságán is megmutatkozott, a hibát általában 20-30 százalékosra becsülték a versenyzõk.


