Folyadékok és gázok mechanikája » Csepegő vízcsap

Jelenség leírása

Egy rosszul elzárt vízcsapból lecseppenõ cseppek látszólag egyenlõ idõközönként követik egymást. Figyeljük meg hosszabb idõn keresztül ezt a jelenséget! Milyen módon jellemezhetjük az idõközök különbözõségét?

Eszközök

stopper

Magyarázat

M. 211. Egy rosszul elzárt vízcsapból lecseppenõ cseppek látszólag egyenlõ idõközönként követik egymást. Figyeljük meg hosszabb idõn keresztül ezt a jelenséget! Milyen módon jellemezhetjük az idõközök különbözõségét?

Megoldás. A csöpögõ csap cseppenéseinek idõpontjai (valamely önkényesen kiválasztott kezdõponttól számítva) stopperral, számítógép belsõ órájának felhasználásával, vagy fénykapu segítségével meghatározhatók, s az idõpontok különbségébõl a cseppek ,,követési távolsága'' kiszámítható. A feladat ezen idõközök mérése és jellemzése (tehát a mérési adatok feldolgozása, áttekinthetõ csoportosítása és bemutatása) volt.

A feladat szövege utalt rá, hogy az idõközök látszólag egyenletesek, érdemes volt tehát az idõtartamok ingadozásait vizsgálni. A véletlenszerûen változó jelenségek tanulmányozásakor a sok mérés átlagolása csökkenti az ingadozásokat; ez a mérés kiértékelésénél általában hasznos, hacsak nem éppen az ingadozások vizsgálata a mérés célja. Sok versenyzõ több (5-10) vízcsepp lecseppenésének összidejét mérte, vagy meghatározott idõ (mondjuk 1 perc) alatt lecseppenõ cseppek számát adta meg, s ezekbõl számolt átlagos idõkülönbséget. Így viszonylag könnyen jutottak meglehetõsen pontos átlagolt idõtartamokhoz, de eközben elmosódott a cseppek idõközeinek egyedi változása, ingadozása.

A mérés pontosságát az idõmérés pontossága határozza meg. Hacsak nem áll rendelkezésünkre automatizált berendezés (pl. fénykapuval vezérelt elektronikus idõmérõ), akkor célszerû a mérési hiba csökkentése érdekében ,,apró trükköket'' alkalmazni. Soós Péter (Kiskunhalas, Bibó I. Gimn., 10. o.t.) a következõ módon járt el. Egy teljes napig tartó mérése során a vízcsapot csak egyszer állította be, a továbbiakban nem ért hozzá. A vízcseppek alá egy felfordított, üres vajasdobozt állított, hogy a leérkezõ vízcsepp hangosan koppanjon, így füllel is érzékelhetõvé váljon. Feltételezte, hogy a vízcsap csepegésének üteme függ a hálózati víznyomástól (ami a többi lakás vízfogyasztásától is függõen ingadozik). Egy kémcsõbõl és egy meghajlított vékony gumicsõbõl egyszerû berendezést állított össze, amellyel folyamatosan figyelni tudta a víznyomás ingadozását. A kémcsõbe (egy másik csapból) vékony sugárban folyamatosan vizet engedett, az egyik végével a vízbe merülõ gumicsövön keresztül pedig kifolyhatott a víz a kémcsõbõl. A kifolyás sebessége függ a vízszint (egyensúlyi) magasságától, annak könnyen leolvasható értékébõl pedig a befolyó víz sebességére, tehát a hálózati víznyomásra lehet következtetni.

A mérési adatok (idõkülönbségek) birtokában a következõ lépés az adatok feldolgozása, kiértékelése. A legtöbben a cseppenések sorszámának vagy a mérés kezdete (a csap beállítása) óta eltelt idõnek a függvényében adták meg (ábrázolták) az idõkülönbségek alakulását. Megállapították, hogy az idõtartamok általában növekednek, tehát a cseppek egyre ritkábban követik egymást. Ez a tendencia nyilván nem folytatódhat sokáig. Gáspár Merse Elõd (Fazekas M. Fõv. Gyak. Gimn., 12 o.t.) azt tapasztalta, hogy az idõtartamok a cseppenések számának függvényében egy darabig monoton (nagyjából egyenletesen) növekednek, majd hirtelen lecsökken a két egymás utáni csepp közötti idõkülönbség, ezután pedig ismét egyenletesen növekszik, s több fûrészfog'' majdnem periodikusan követi egymást.

Másféle kiértékelési eljárást választott Geresdi Attila (Pécs, Árpád Fejedelem Gimn., 10. o.t.). Az n+1-edik cseppenés utáni tn+1 idõközt ábrázolta az elõzõ tn függvényében. A mérési eredmények a tn+1(tn) síkon különbözõ n-ekre pontok, vagy ha a mérési hibát is érzékeltetni akarjuk, akkor kis téglalapok lesznek. Ha a cseppek (közel) egyenlõ idõközökben követik egymást, akkor a pontsereg kis területen (egy kupacban) található. A pontkupac a diagram 45o-os egyenesén helyezkedik el, a csap elzártságától függõ helyen. Ezt mutatja az (1. ábra). Ha a csapot annyira elzárjuk, hogy a cseppek kb. 0,2 s idõközökben követik egymást, a kép lényegesen megváltozik. A mérési pontok a tn+1(tn) diagramon egy nagyobb tartományban szétszórva, ,,összevissza'' helyezkednek el, a vízcseppek ,,kaotikusan'' követik egymást (2. ábra). A szabályos és a kaotikus tartományt közötti átmenetet a 3. ábrán látható grafikonnal is illusztrálta Geresdi Attila. Ezen a cseppek közötti átlagos idõtartam és az átlag körüli relatív ingadozás (relatív szórás) látható. Megfigyelhetjük, hogy 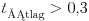t_{\text{átlag}}>0{,}3 s esetén a relatív ingadozás viszonylag kicsi és állandó, ha viszont 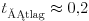t_{\text{átlag}}\approx0{,}2 s, az ingadozás lényegesen nagyobb.

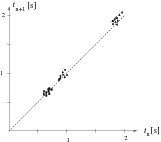
1. ábra

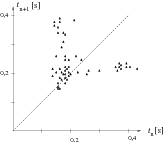
2. ábra

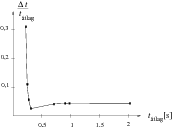
3. ábra

Mások is megfigyelték, hogy bizonyos esetekben (bizonyos csapnyílás esetén) a cseppek úgy követik egymást, hogy az idõközök periodikusan váltakozva egy rövidebb és egy hosszabb érték között ,,ugrálnak''. Coc Károly (Marosvásárhely, Bolyai F. Líceum 9. o.t.) egy kis villanymotor segítségével papírszalagot húzott el a vízcsap alatt. A vízcseppek nyomot hagytak a papírszalagon. A nyomok távolságát utólag lemérte, majd kiszámította a vízcseppek idõkülönbségeket. Azt tapasztalta, hogy az átlagos vízhozamtól függõen a cseppek többé-kevésbé egyenletesen is csepeghetnek, de (nagyobb vízhozamnál) rendszertelenül, szemmel láthatóan erõsen ingadozva is követhetik egymást.

Úgy is lehetett volna jellemezni az idõtartamokat, hogy megadjuk az ,,eloszlásukat''. Ez annyit jelent, hogy bizonyos számú (lehetõleg jó sok) mérési adatot aszerint osztályozunk, hogy mennyi esik közülük egy bizonyos (pl. az 5 és az 5,5 másodperc közötti) idõintervallumba. Az eloszlásdiagram ,,szélessége'' az ingadozásokra jellemzõ, az egymás utáni idõközök közötti kapcsolatot (az ún. korrelációt) azonban nem mutatja meg.

!!\small!!Megjegyzés. A cseppek követési idejének változatos alakulását több (részben még nem eléggé ismert) jelenség okozhatja. A kérdésrõl és a kaotikus jelenségek különbözõ megközelítési módjairól részletesebben olvashatunk I. Stewart: A természet számai (A matematikai képzelet irreális realitása) címû könyvében (Kulturtrade Kiadó, 1995.).

Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Gáspár Merse Elõd
  • Geresdi Attila
  • I. Stewart: A természet számai
  • Soós Péter
  URI STRING  
/show/211/F-B-G
  CLASS/METHOD  
show/index
  MEMORY USAGE  
619,488 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0004
Controller Execution Time ( Show / Index )  0.0106
Total Execution Time  0.0110
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0006   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('17e186323f33737e5e79a467422a0074', '3.133.144.147', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1732411090) 
0.0008   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0006   SELECT *
FROM (`experiments`)
WHERE `eid` = '211' 
0.0008   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '211' 
0.0004   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '211' 
0.0004   SELECT `name`
FROM (`materials`)
WHERE `eid` = '211' 
0.0002   SELECT `source`
FROM (`sources`)
WHERE `eid` = '211' 
0.0003   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '211' 
0.0003   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '211'