Jelenség leírása
Széles mérõhengerben függõleges helyzetben úszik a vizen egy kémcsõ, amelynek alján nehezék (pl. víz, sörét, homok) van. Ha a kémcsövet kissé megemeljük, majd elengedjük, függõleges irányú csillapodó rezgõmozgást végez. Mérjük meg (különbözõ terhelések esetén) a T rezgésidõt!
Eszközök
kémcsövek, nehezékek, stopper, vonalzó
Magyarázat
M. 210. Széles mérõhengerben függõleges helyzetben úszik a vizen egy kémcsõ, amelynek alján nehezék (pl. víz, sörét, homok) van. Ha a kémcsövet kissé megemeljük, majd elengedjük, függõleges irányú csillapodó rezgõmozgást végez. Mérjük meg (különbözõ terhelések esetén) a T rezgésidõt és számítsuk ki az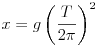 
mennyiség értékét! Hasonlítsuk össze x-et a nyugalomban lévõ kémcsõ vízbe merülõ részének hosszával!
Megoldás. A kémcsõ úszási stabilitása érzékenyen függ a súlypontjának helyzetétõl. Minél nagyobb sûrûségû a nehezék, annál mélyebben lesz a rendszer súlypontja, s annál stabilabban úszik. Célszerû tehát sörétet (vagy egyéb ólomdarabkákat) helyezni a kémcsõ aljába, ,,víznehezékkel'' a kémcsõ oldalirányú lengése, billegése zavarja a mérést.
A kémcsõ merülési mélysége az egyensúlyi helyzetben milliméter pontossággal mérhetõ, az aljának görbülete azonban kérdésessé teszi, hogy melyik pontját tekintsük a csõ legaljának.
A függõlegesen kitérített kémcsõ erõsen csillapodó rezgõmozgást végez, emiatt 5-6 lengésnél több nem (vagy csak igen nehezen) figyelhetõ meg. (Voltak versenyzõk, akik 20 lengés idejébõl számoltak periódusidõt, legalábbis a beszámolójuk szerint! Eljárásuk elvben helyes, de a gyakorlatban megvalósíthatatlan! A mérési feladatoknál ténylegesen elvégzett mérésekrõl szóló beszámolót várunk, nem pedig elképzelt módszerek, esetleg vágyálmok leírását.)
A lengési periódusidõ meghatározását nehezíti a kémcsõ billegése, a függõleges rezgés és az oldalirányú periodikus elfordulások összecsatolódása. Nagy Ádám (Budapest, Szent István Gimn., 11. o.t.) 2 egyforma pezsgõtablettás dobozt erõsített össze, majd nehezékekkel látta el azokat. Így viszonylag mélyre került a tömegközéppont, a ,,táncolást'' szinte teljesen meg tudta szüntetni és nagy (kezdetben 10 cm-es) amplitúdójú lengéseket is megfigyelhetett. Patay Gergely (Debrecen, Tóth Á. Gimn., 12. o.t.) egy Bunsen-állványba befogott üvegrudat lógatott felülrõl a kémcsõbe, így akadályozta meg a csõ eldõlését (jóllehet a súrlódás a lengések csillapodását növelte).
A T rezgésidõ mérési pontossága néhány tizedmásodpercre tehetõ, de ez csak úgy érhetõ el, ha minden terhelésnél többször (legalább 5-ször, vagy akár 10-szer) mérünk, s a mért értékek átlagát képezzük. (Többen alkalmazták ,,a legnagyobb és a legkisebb mért adatot nem vesszük bele az átlagba'' módszert. Ez bizonyos sportversenyek pontozásánál elfogadható, de fizikai méréskiértékelésnél nem indokolt eljárás. Minden elvégzett mérés eredménye (akármennyire váratlan, a többitõl eltérõ is az) tartalmaz információt a mért mennyiségrõl, tehát figyelembe kell venni. Ha a szokatlan eredményt mérési hiba okozza, azt úgy vesszük észre, hogy többször ismételve a mérést nem tapasztaljuk újra, így az átlag számítása során nem (vagy csak megfelelõen kis mértékben) szól bele a végeredmény kialakításába.
A mérés eredménye (minden egyes terhelésnél az átlag képzése után) egy számpárral, a T-bõl kiszámítható x-szel és az ugyancsak mérés eredményeként adódó y merülési mélységgel adható meg. Érdemes a mérési eredményeket az x-y koordináta rendszerben pontokkal, vagy a mérési hiba nagyságrendjére utaló ,,keresztekkel'' megadni. Az eredmények azt mutatták, hogy kb. 10 százalék pontosságon belül teljesül az x=y összefüggés, amit bizonyos elméleti megfontolások is alátámasztanak. (Ha a kémcsõre ható erõt egyszerûen a pillanatnyi merülési mélységnek megfelelõ felhajtóerõbõl számítjuk, olyan rezgõmozgás egyenletét kapjuk, melynek megoldása éppen y=x-nek felel meg. Meglepõ, hogy ez az erõsen leegyszerûsített kép, amely nem veszi figyelembe pl. a kémcsõ által megmozgatott vízmennyiség tehetetlenségébõl adódó fékezõ hatást, a mérési adatokkal mennyire jól egyezõ jóslatot ad.)
Gondosabb és pontosabb mérések megmutatták, hogy x szisztematikusan eltér y-tól. A lengésidõbõl számított x nagyobb a bemerülési mélységnél, méghozzá annál inkább eltér attól, minél nagyobb a nyugalomban levõ kémcsõ vízbe merülõ részének hossza. Sebestyén Zsolt (Pécs, Apáczai Csere J. Gimn., 11. o.t.) mérési adatai azt mutatták, hogy az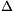 
x=y-x különbség a merülési mélységgel közel lineárisan változott, y=123 mm-nél 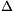x csak 7 mm volt, y=155 mm-nél azonban az eltérés már 40 mm-re nõtt.
Lipcsei Gábor (ELTE Radnóti M. Gyak. Gimn. 11. o.t.) a kémcsõ által mozgásba hozott víz többlettömegével magyarázta a lengésidõ (és ezzel együtt a kiszámított x mennyiség) vártnál nagyobb értékeit. Megfigyelte, hogy a lengésidõ (a szokásos harmonikus rezgõmozgástól eltérõen) függ a lengés amplitúdójától is: nagyobb kezdeti kitérésnél (amikor nyilván több vizet mozgat meg a kémcsõ) a rezgésidõ egy kicsit nagyobb volt, mint a kisebb amplitúdójú mozgásnál. Különbözõ vastagságú kémcsövekkel is végzett méréseket, és megállapította, hogy vékonyabb kémcsõnél x és y eltérése kb. 7-9%, vastagabb kémcsõnél azonban ez az eltérés csak 2-3%. Sejtését (miszerint ez a tendencia más mérettartományban is folytatódik) további kísérletekkel igazolta. Egy hosszú mûanyag tollból eltávolította a betétet, majd éppen beleférõ söréttel megterhelte. Ennél az igen karcsú ,,kémcsõnél'' az 1-2 százalékos mérési hibahatáron belül nem tapasztalt eltérést x és y között.
