Jelenség leírása
Mérjük meg minél pontosabban a pingponglabda anyagának sûrûségét! Becsüljük meg mérésünk pontosságát!
Eszközök
mérleg, pingponglabda, Vízzel telt magas mérőhenger, vonalzó
Magyarázat
A sûrûség mérése elvben visszavezethetõ tömeg és térfogat mérésére. A tömeg kellõen pontos mérleggel könnyen megoldható. (Több versenyzõ is közeli gyógyszertárba ment be, és ott kérte, hogy mérjék meg a patikai mérlegen a pingponglabda tömegét.) A térfogat mérése sem látszik nehéz feladatnak, ha egy szabályos test (pl. egy gömb) térfogatát kell meghatároznunk. Tolómérõvel vagy mikrométerrel tized- vagy századmilliméter pontossággal lemérhetõ egy pingponglabda külsõ átmérõje. (Sokan rájöttek, hogy ilyen pontosság mellett már egyáltalán nem biztos, hogy a labda ,,gömbölyû''; a különbözõ irányokban mért átmérõje általában eltérõ nagyságúnak adódik.)
Többen félreértették a kérdést, és a sûrûségét a labda tömegének és a külsõ átmérõbõl számított gömb térfogatának hányadosaként adták meg. Ez a mennyiség a labda és a benne levõ levegõ átlagsûrûségét adja meg (kb. 0,1 g/cm3-t), ami nyilvánvalóan különbözik a labda anyagának sûrûségétõl. Az is hibásan járt el, aki a labda mérlegen mért tömegébõl kivonta a benne levõ levegõ (labda térfogatából és a levegõ sûrûségébõl kiszámítható) tömegét. A mérleg ugyanis nem méri a labdában levõ levegõt, hiszen annak súlya éppen akkora, amekkora felhajtóerõ hat a labdára a környezõ levegõ miatt. (Feltételezhetjük, hogy a labdában levõ levegõ ugyanakkora sûrûségû, mint a külsõ légkör, továbbá, hogy a labda falának térfogata sokkal kisebb, mint a bezárt levegõé.)
A labda falának sûrûségét a fal térfogatának ismeretében tudjuk kiszámítani. Sok versenyzõ félbe (vagy még kisebb darabokra) vágta labdát, s közvetlen méréssel (tolómérõvel), vagy közvetett úton (a belsõ és a külsõ átmérõ mért különbségébõl) határozta meg a labda anyagának térfogatát. Mindkét módszer meglehetõsen pontatlan, hiszen a labda fala viszonylag vékony, így a relatív hiba 20-30% vagy még ennél is több lehet. Két - majdnem egyforma átmérõjû - gömb térfogatának különbsége sokkal kisebb, mint a gömbök térfogata, emiatt hiába ismerjük külön-külön viszonylag pontosan a gömbök átmérõjét (térfogatát), a különbség relatív bizonytalansága sokkal nagyobb lesz. A közvetlen vastagságmérést az is nehezíti, hogy a mikrométer henger alakú mérõfelülete nem fekszik fel a szétvágott labda belsõ oldalára. Ezt a problémát úgy lehetett volna megoldani, hogy egy kicsiny csapágygolyót érintünk belülrõl a labdához, s ezzel együtt mérjük meg a vastagságot, majd a mért értékbõl kivonjuk a csapágygolyó elõzõleg megmért átmérõjét.
A ,,gömbhéj'' térfogatának mérése a fentebb leírt módon még akkor is megkérdõjelezhetõ, ha kellõ gondossággal végezzük el a falvastagság mérését. Többen felfigyeltek rá, hogy a labda fala nem egyenletes vastagságú, a mért vastagságadatok számottevõ ,,szórást'' mutatnak. Ehhez járul még a két félgömbhéj összeragasztásánál megfigyelhetõ ,,abroncs'', melynek extra járulékát többen megpróbálták számítással figyelembe venni.
Helyesebben jártak el azok, akik a labda falának térfogatát úgy mérték meg, hogy nem tettek semmiféle elméleti megfontolást a fal geometriai alakjára. Kállai Márton (Budaörs, Illyés Gy. Gimn. 12. o.t.) nyolc darabra vágott fel egy pingponglabdát, majd az összes darabot mérõhengerbe rakta. (Vigyázott rá, hogy a darabokat egymás után helyezze a hengerbe, nehogy levegõ maradjon közöttük.) A mérõhengerrel mérni tudta a kiszorított víz térfogatát, ami (hacsak nem maradt parányi légbuborék a mûanyagdarabkákon) megegyezik a labda falának térfogatával. Mérése szerint a labda anyagának sûrûsége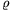 
=1,06 g/cm3, és a mérés pontosságát (a tömegmérés és a térfogatmérés pontosságából) 5%-ra becsülte. A mérés pontossága fokozható, ha a mérés elõtt gondosan zsírtalanítjuk a labda darabkáit, ismert hõmérsékletû, kiforralt desztillált vízzel dolgozunk, és a folyadék térfogatának mérését felül elkeskenyített mérõedénnyel végezzük.
Sokan végeztek elõzetes sûrûség-becslést úgy, hogy a pingponglabda darabkáit vízbe dobták, s megfigyelték, hogy a darabkák lassan lesüllyednek. Ebbõl arra következtettek, hogy a labda anyagának sûrûsége egy kevéssel nagyobb, mint a víz sûrûsége. Bálint László (Temesvár, Bartók B. Líceum 10. o.t.) fokozatosan növelt koncentrációjú sós vizes oldatot készített, s figyelte, hogy elsüllyednek, felszállnak vagy éppen lebegnek-e az oldatban a pingponglabda darabkái. A határesetnek megfelelõ töménységû sóoldat sûrûségét aerométerrel (úszó sûrûségmérõvel) viszonylag pontosan meg tudta mérni, s a mért érték megadta a labda anyagának sûrûségét is.
Hasonló módon járt el Flender Gyöngyi (Hajdúszoboszló, Hõgyes E. Gimn. 10. o.t.) is, aki a vasárnapi ebéd készítése közben figyelt fel arra, hogy a húslevesben a tésztagombócok a sózottságtól (és a hõmérséklettõl) függõen úsztak, lemerültek vagy éppen lebegtek. A pingponglabda darabkáinak sûrûségét gyorsan oldódó sóból készített (a határesetnek megfelelõ) oldat térfogatának és tömegének mérése után számítással határozta meg. Megfigyelte, hogy a pingponglabda nem minden része azonos sûrûségû. Azok a darabkák, melyek összeragasztott részt is tartalmaztak, még úsztak akkor, amikor a labda többi része lebegett. (Ez a ragasztó kisebb sûrûségével, vagy az összeragasztott részek között maradt parányi légbuborékokkal magyarázható.)
A legügyesebben (és legeredményesebben) Nagy Ádám (Budapest, Szent István Gimn. 11. o.t.) oldotta meg a feladatot. Abból indult ki, hogy az iskola kémia laboratóriumában található korszerû mérleggel ezred grammnál is pontosabban (!) lehet tömeget (és súlyt) mérni. Ez a pontosság sokkal jobb, mint a térfogat- vagy hosszúságméréseknél elérhetõ mérési hibahatár, érdemes tehát olyan módszert keresni, amely tisztán tömegmérésbõl áll. Az érzékeny mérleggel lemérte egy desztillált vízzel félig töltött pohár súlyát, majd megismételte a mérést úgy, hogy egy rögzített állványra kötött fonálon a vízbe lógatta a félbevágott pingponglabda darabjait. A labda darabkáira a kiszorított víz súlyának megfelelõ felhajtóerõ hat, ennek az erõnek az ellenereje viszont a vizet (a poharat és rajta keresztül a mérleget) nyomja lefele. A második mérésnél tehát a mérleg az elsõ méréshez viszonyítva éppen annyival mutatott többet, amennyi a labda anyaga által kiszorított víz tömege. Ebbõl az adatból (és a hõmérsékletbõl) a víz sûrûségének ismeretében kiszámítható a labda falának térfogata, az elõzõleg megmért tömegébõl pedig a sûrûsége.
Hasonló módon végezte el a mérést Pozsgay Balázs (Pécs, Magyar-német Nyelvû Isk. 11. o.t.) is, de õ nem állványról lógatta le, hanem kézzel tartotta a (kilyukasztott) pingponglabdát. Ilyenkor a kéz kicsiny remegése okoz mérési hibát. (A vízben mozgó testre közegellenállási erõ hat, melynek ellenerejét az érzékeny mérleg ingadozások formájában jelzi.) Érzékeny mérleg használatakor célszerû rezgésmentes körülményeket biztosítani, pontosabban fogalmazva: a környezetbõl származó rezgéseket olyan mértékben csökkenteni, amennyire csak lehet.)
!!\small!!Megjegyzés. A mérési feladat értékelésénél az kaphatja meg a maximális pontszámot, aki ötletes mérési módszer választ, az alkalmazott módszert világosan, áttekinthetõen leírja, elegendõ számú és pontosságú, tényleges mérésbõl származó adattal rendelkezik és azokat áttekinthetõ táblázatba rendezi vagy grafikonon ábrázolja, a mérési adatokból a keresett mennyiséget meghatározza, és végül korrekt hibaszámítással elfogadható becslést ad a mérés pontosságára. Az a megállapítás, hogy ,,a mérés nem tökéletesen pontos'' (melyik mérés az?), vagy annak kijelentése, hogy ,,a mérõeszközök hibája miatt a mérésem nem túl pontos'', önmagában nem fogadható el hibabecslésként, de még az sem, ha valaki (indoklás nélkül) közli: ,,véleményem szerint az eredményem 10 százalékra pontos''. Ugyancsak értékelhetetlenek a mérési eredményeket nem tartalmazó, csak elvi leírást közlõ dolgozatok, továbbá azok, melyek különbözõ tanulók tökéletesen azonos mérési módszerérõl és azonos mérési eredményeirõl számolnak be.
