Geometriai optika » Távcső nagyítása

Jelenség leírása

Határozzuk meg, hogy egy színházi látcsõbe nézve milyen irányban lévõ tárgyakról láthatunk képeket és mekkora a nagyítás! Függ-e a nagyítás a tárgy távolságától?

Eszközök

színházi távcső, vonalzó

Magyarázat

Hegedûs Ákos (Pécs, Ciszterci Nagy Lajos Gimn., 10. o.t.) egy deszkára zsírkrétával 5 cm-enként jeleket tett, majd megfigyelte, hogy különbözõ távolságokban elhelyezve a deszkát annak mekkora darabja ,,fér bele'' a látcsõ látómezejébe. A deszka távolságát mérõszalaggal mérte, majd kiszámította a látószöget. A távolságmérések hibájának nagyságrendjébõl becslést adott a kiszámított látószög mérési hibájára is. A nagyítást úgy mérte meg, hogy elkészítette a távcsõ mérethû vázát kartonpapírból, majd megismételte az elõzõ látószögmérést a lencse nélküli ,,távcsõvel''. A két látószög aránya megadja a szinházi távcsõ szögnagyítását. 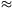Azt tapasztalta, hogy a t tárgytávolság növelésével az N szögnagyítás kis mértékben csökken: 2-6 m-nél N\approx2,5, míg 10-18 m-es tárgytávolságoknál N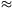\approx2,0. Ugyanilyen jellegû távolságfüggést figyelt meg Ivády Balázs (Kazincbarcika, Ságvári E. Gimn., 11. o.t.) is, és ezt a látcsõ élességbeállítási lehetõségének tulajdonította. Mások azt tapasztalták, hogy a szögnagyítás a mérési hibahatáron belül nem függ a tárgy távolságától.

Péterfalvi Csaba (Szekszárd, Garay J. Gimn., 11. o.t.) egy diavetítõ segítségével ,,pontszerû fényforrást'' hozott létre. Egy üveges diakeretbe olyan alumíniumfóliát helyezett, melyen elõzõleg egy tûvel kicsiny lyukat szúrt. Ezen a lyukon áthatoló fénysugarat (keskeny sugárnyalábot) keresztülbocsátotta a távcsövön, és mérte annak szögeltérülését egy fekete ernyõ segítségével. Azt tapasztalta, hogy a szögnagyítás a távcsõ tengelyéhez viszonyított szög függvényében 6o körül gyenge minimumot mutatott, és ebbõl a távcsõ leképezési hibáira következtetett.


Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Hegedûs Ákos
  • Péterfalvi Csaba
  URI STRING  
/show/193/F-I-B
  CLASS/METHOD  
show/index
  MEMORY USAGE  
603,472 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0004
Controller Execution Time ( Show / Index )  0.0093
Total Execution Time  0.0097
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0007   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('9f52df96c2477861b4b311b6d32991fe', '18.189.180.244', 'claudebot', 1713487976) 
0.0006   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0008   SELECT *
FROM (`experiments`)
WHERE `eid` = '193' 
0.0006   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '193' 
0.0004   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '193' 
0.0006   SELECT `name`
FROM (`materials`)
WHERE `eid` = '193' 
0.0005   SELECT `source`
FROM (`sources`)
WHERE `eid` = '193' 
0.0006   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '193' 
0.0005   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '193'