Jelenség leírása
Ha a nyomógombos golyóstollat gombbal lefelé az asztalhoz nyomjuk, majd elengedjük, azt tapasztaljuk, hogy a toll kissé felugrik az asztalról. Mérjük meg, mekkora mozgási energiát ad a rugó a tollnak!
Eszközök
golyóstoll, vonalzó
Magyarázat
Az elvben egyszerû mérésnél gondot általában a magasság pontos meghatározása okozta. A legegyszerûbb - de nagyon pontatlan - módszer az, ha egy függõlegesre állított vonalzó elõtt felugró tollat oldalról ,,szemlélve'' próbáljuk meg leolvasni az emelkedési magasságot. Mivel ez 1-2 cm nagyságrendû, a leolvasási pontatlanság néhány milliméter lévén a magasságmérés hibája még sokszori ismétléssel és átlagolással sem szorítható 20-30 százalék alá. A mért energiák - természetesen a toll típusától is függõen - általában néhány mJ-nak adódtak.
Sutka Melinda (Debrecen, KLTE Gyak. Gimn. II. o.t.) vízszintesen helyezett el egy vonalzót a felugró toll fölé, úgy, hogy az éppen megérintse a vonalzót. Ezt követõen nyugodt körülmények között megmérte a vonalzó magasságát és abból kivonva a toll hosszát megkapta az ugrás magasságát.
Sarlós Ferenc (Baja, III. Béla Gimn. III. o.t.) közvetett módon határozta meg a rugó által leadott energiát. Két fadeszkából lejtõt készített, melynek hajlásszögét változtatva megmérte toll egyenletes csúszásához tartozó ,,határszöget'', ennek tangense pedig megadta a toll és a deszka közötti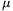 
csúszási súrlódási együtthatót. Ezután a vízszintesre állított deszkán kilõve a tollat az elcsúszás távolságából, a toll mérlegen megmért tömegébõl és a súrlódási együtthatóból kiszámította a súrlódási munkát, ami a kezdeti mozgási energiával egyenlõ. Ezzel a módszerrel mérni tudta a golyóstoll rugója által leadott energiát mindkét nyomógomb-állásnál (a toll be- illetve kinyomásának megfelelõ helyzetnél).
Orosz Gábor (Miskolc, Földes F. Gimn. IV. o.t.) a mérést különbözõ mértékben benyomott nyomógombú tollak emelkedési magasságát mérte (ugyancsak az ,,éppen hozzáér'' módszerrel, s a mérési adatokból meghatározta a toll nyomógomb-rugójának direkciós állandóját. Drávucz Mónika (Eger, Szilágyi E. Gimn. III. o.t.) rugós erõmérõvel lemérte a toll rugójának rugóállandóját, majd az abból és az összenyomás nagyságából kiszámított rugalmas energiát összehasonlította a felpattanási magasságból számított energiával. Az két energia között 15%-nyi eltérést talált, ráadásul a rugalmas energia volt a kisebb, ez azonban nem jelenti az energiamegmaradás tételének cáfolatát, inkább a mérési hibák nagyságrendjérõl ad felvilágosítást. Zágoni Csaba (Dunaújváros, Széchenyi I. Gimn. I. o.t.) egy lámpa vízszintes fénynyalábját vetítette a felugró tollra, s az árnyékot 5-szörös nagyításban egy függõleges ernyõn figyelte meg. Az így felnagyított mozgás felsõ holtpontját pontosabban tudta leolvasni, mintha közvetlenül a tollat figyelte volna meg.
Az eddig leírtaktól alapvetõen különbözõ mérési eljárást választott Friedl Zita (Sopron, Széchenyi I. Gimn. I. o.t.). Egy vízszintes asztallap szélérõl (a toll tömegközéppontját éppen az asztal pereméig kitolva) ,,lõtte ki'' a golyóstollat, és azt mérte meg, hogy milyen távolságban esik le a toll egy h=15 cm-rel alacsonyabb fekvõ vízszintes lapra. A vízszintes hajítás képletei segítségével a mért adatokból ki tudta számítani a golyóstoll kezdõsebességét és a kezdeti mozgási energiáját is. A módszernek az az elõnye, hogy viszonylag nagy távolságokat pontosabban lehet mérni, mint néhány centiméteres elmozdulásokat. Hasonló elvet alkalmazott Szegedi Krisztián (Bp., Berzsenyi D. Gimn. IV. o.t.) is, aki egy szekrény függõleges oldalától lõtte ki vízszintesen a tollat, és a szõnyegen mérte a földetérés helyét. Emellett gyenge rugóból erõmérõt is készített s azzal megmérve a toll nyomógombjának rugóállandóját kiszámította a rugóban tárolt energiát.
Még bátrabban eltávolodott az eredeti feladattól Varró Gergely (Fazekas M. Fõv. Gyak. Gimn. IV. o.t.), aki vízszintes helyzetben rögzítette a golyóstollat egy asztal szélén, és a kipattanó nyomógombbal egy kisméretû dobókockát röpített el. A földetérõ dobókocka rögzített helyzetû, fölülrõl másolópapírral lefedett papírlapra csapódott és azon nyomot hagyva jelezte a vízszintes hajítás távolságát. A kocka mérhetõ tömegébõl és a hajítás adataiból ki lehet számítani a rugó által leadott energiát. Elfogadható feltételezés az, hogy a rugó munkavégzése csak a rugó jellemzõitõl és a deformáció mértékétõl függ, nagysága tehát a dobókocka kilövésekor ugyanakkora, mint amikor a golyóstollat hozza mozgásba.
