Tömegpont dinamikája » Gumi erő-megnyúlás karakterisztikája

Jelenség leírása

Határozzuk meg egy adott hosszúságú kalapgumi erõ-megnyúlás karakterisztikáját! Mérjük meg különbözõ terhelések mellett a kis függõleges kitérésû rezgések frekvenciáját! Milyen kapcsolatba hozható a frekvencia-terhelés függvény a karakterisztikával?

Eszközök

Állvány (vízszintes rúddal), hosszú vonalzó vagy mérőszalag

Magyarázat

,,A rövidárú boltban kalapgumi néven kapható fehér és fekete színû, lapos vagy hengeres rugalmas szál'' eredeti rendeltetésérõl Sáfrány Ilona Virág (Debrecen, Irinyi J. Szki., 11. évf.) tudósít dolgozatában kellõ részletességgel. ,,Bár a kalap, kalpag mindkét nem viseletében régmúlt idõkig nyúlik vissza, a láthatatlan (alig látható) rögzítés viszonylag újkeletû, ... fénykorát kb. az 1950-es évekre tehetjük. ... elõnye, hogy úgy tudja rögzíteni a kalapot a fejhez, hogy a gumit el lehetett rejteni a haj alá, közé, színében is illeszkedve viselõje haj-, kalap színéhez és korához.''

A feladat mérési részének elvégzése nem okozott különösebb gondot a feladat beküldõinek. Jóllehet a feladat szövege adott hosszúságú kalapguminál kérdezte a megnyúlás-erõ és a rezgési frekvencia-terhelés karakterisztikák meghatározását, néhányan több különbözõ hosszúságú gumira is elvégezték a mérést. A felfüggesztés és a terhelés módját sem kötötte meg a feladat, mégis mindenki az egyik végénél rögzített és a másiknál függõlegesen terhelt gumit vizsgálta. Sáfrány Ilona Virág ezen elrendezés mellett a vízszintes, mindkét végénél rögzített és a közepén terhelt gumival is elvégezte a mérési sorozatot.

Mindenki észlelte, hogy a gumiszál megnyúlása a terhelés függvényében nem reverzibilis folyamat; a nehezékek leszedése után minden gumiszálban valamekkora maradandó alakváltozás (maradandó deformáció) marad. Ezt a ,,hiszterézisszerû'' jelenséget szemlélteti a Mezei Márk (Budapest, ELTE Radnóti M. Gyak. Gimn., 12. évf.) által felvett megnyúlás-terhelés grafikon (1. ábra). (A feladat nem kérte a fordított folyamat tanulmányozását.)

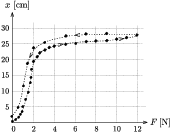
1. ábra. Egy gumiszál megnyúlása-erõ karakterisztikája

Ezen karakterisztikák igen hasonlóan néztek ki a különbözõ beküldött dolgozatokban; mutatkozott bennük egy görbületváltás (inflexiós pont), és jellegzetes tulajdonságuk, hogy ,,ellaposodnak'', vagyis hogy nagy terheléseknél a szál megnyúlása szinte változatlanná, a terheléstõl függetlenné válik. Többen felfigyeltek arra, hogy a gumiszál a súly ráakasztása után még egy bizonyos ideig (Mezei Márk szerint kb. még egy percig) nyúlik.

A mérés második részét - a rezgési frekvencia terheléstõl való függésének vizsgálatát - vagy az elsõ méréssel együtt, vagy utána végezték, ez utóbbi esetben a maradandó alakváltozás miatt új gumiszálakkal. Többen is megemlítették, hogy a rezgések gyors csillapodása nehezítette a mérést. A mérési eredmények alapján kapott frekvencia-terhelés görbe is igen egységesnek bizonyult a különbözõ dolgozatokban; mutatkozik benne egy jellegzetes minimum. Mezei Márk mérési adatait a 2. ábra mutatja.

2. ábra. Rezgési frekvencia-terhelõerõ karakterisztika

A feladat harmadik része - a két karakterisztika közötti kapcsolat megtalálása - már csak keveseknek sikerült. Arra többen rájöttek, hogy a gumi ,,direkciós állandója'' nem igazán állandó, hanem a terhelés (vagy akár a megnyúlás) függvényében változó mennyiség; és ezt a kapcsolatot meg is határozták. Szabó Áron (Debrecen, Fazekas M. Gimn., 12. évf.) pl. a megnyúlás-erõ karakterisztika pillanatnyi (az erõ aktuális értékéhez tartozó) iránytényezõjének reciprok értékét, vagyis a 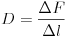D=\frac{\Delta F}{\Delta l} mennyiséget határozta meg, Varga Lajos (Gyula, Karácsonyi János Kat. Gimn., 11. évf.) pedig a rezgési idõkbõl számolt direkciós állandót a 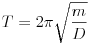T=2\pi \sqrt{\frac{m}{D}} képlet alapján.

Mezei Márk és Szabó Áron lényegében hasonlóképpen jártak el, amikor a már említett módon (az erõ-megnyúlás karakterisztika meredekségébõl) meghatározott direkciós állandóból kiszámították az aktuális terhelésnek megfelelõ ,,elméleti'' rezgési frekvenciákat. A 3. ábrán ezek láthatók (ugyancsak Mezei Márk dolgozata alapján), de a grafikonon az összehasonlítás megkönnyítése érdekében feltüntettük a 2. ábrán már közölt közvetlenül mért frekvencia-értékeket is.

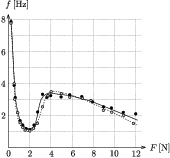
3. ábra. Frekvencia-erõ karakterisztika számított értékei (fekete körök).!!\\!! A szürke körök a frekvencia közvetlenül mért értékeit mutatják

Látható, hogy a két adatsor igen jól egyezik. Szabó Áron számított és mért frekvencia-értékei is csak néhány (legfeljebb 10) százaléknyi eltérést mutatnak.

A többi dolgozatban csak enyhe utalások olvashatók a két grafikon közötti összefüggésre, az érdemi kapcsolat meghatározása hiányzik.

Szerzők

  • Gnadig Péter

Forrás, irodalom, hivatkozás

  • Mezei Márk
  • Szabó Áron
  • Tóth László
  URI STRING  
/show/1252/F-B-C
  CLASS/METHOD  
show/index
  MEMORY USAGE  
619,376 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0006
Controller Execution Time ( Show / Index )  0.0094
Total Execution Time  0.0101
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0004   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('1dd2da1ae518cbbebebd79f6615073f2', '18.218.38.125', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1713934094) 
0.0006   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0007   SELECT *
FROM (`experiments`)
WHERE `eid` = '1252' 
0.0007   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '1252' 
0.0006   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '1252' 
0.0007   SELECT `name`
FROM (`materials`)
WHERE `eid` = '1252' 
0.0007   SELECT `source`
FROM (`sources`)
WHERE `eid` = '1252' 
0.0007   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '1252' 
0.0004   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '1252'