Tömegpont dinamikája » Kúpinga mozgása

Média

Képek

Filmek

Kupinga

Jelenség leírása

A kúpingát indítsuk el, majd vele szinkronban indítsuk el a kúp magasságának megfelelő hosszúságú fonálingát is. A kúpinga és a magasságával megegyező hosszúságú fonálinga lengésideje megegyezik.

Összeállítás

Egymás mellett állítsunk össze egy kúpinga mozgást végző rendszert, és egy olyan hosszú fonálingát, amelynek hossza megegyezik a kúp magasságával.

Eszközök

állvány, Fonál, kisméretű ingatestek.

Magyarázat

116. Kúpinga mozgása

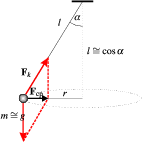
Fonálingát mozgathatunk úgy, hogy az ingatest vízszintes síkú körmozgást végezzen. Ezt az elrendezést nevezzük kúpingának, mert ilyenkor az inga fonala egy egyenes kúp palástját futja be. A kúp fél-nyílásszögét, vagyis a fonál függõlegessel bezárt szögét jelöljük alpha-val, a fonál hosszát l-lel. Számítsuk ki, hogy mekkora a kúpinga periódusideje.

A kúpinga periódusideje egyszerû összefüggésben áll a körmozgást végzõ ingatest szögsebességével: 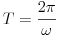T=frac{2pi}{omega}. A szögsebességet a körmozgás dinamikai feltételébõl határozhatjuk meg. Az ingatestre két erõ hat; a függõleges nehézségi erõ és a fonálirányú kényszererõ (fonálerõ). Ezek eredõje szolgáltatja a körmozgáshoz szükséges centripetális erõt. Az ábra alapján jól láthatjuk, hogy az eredõ (centripetális) erõ: mg tg alpha, tehát a mozgásegyenletet így írhatjuk fel:

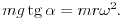
mgmathop{ m tg}alpha=mromega^{2}.

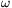A körpálya sugarát is kifejezhetjük az alpha szöggel, továbbá a fonál hosszával (r=lsin alpha), és így meghatározhatjuk az omega szögsebességet, illetve a T periódusidõt:

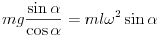
mgfrac{sinalpha}{cosalpha}=mlomega^2sinalpha

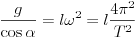
frac{g}{cosalpha}=lomega^2=lfrac{4pi^2}{T^2}

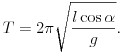
T=2pisqrt{frac{lcosalpha}{g}}.

Vegyük észre, hogy a kapott formula éppen megegyezik az lcos alpha hosszúságú fonálinga lengésidejével. Ez a hosszúság pontosan a kúp magasságával egyenlõ, tehát eredményünk azt mutatja, hogy a kúpingák periódusideje megegyezik a kúpok magasságának megfelelõ hosszúságú fonálinga lengésidejével.


Szerzők

  • Baranyai Klára
  • Honyek Gyula

Forrás, irodalom, hivatkozás

  • Fizika, középiskolai tankönyvsorozat a Műszaki Kiadó gondozásában Szerzők: Gulyás János, Honyek Gyula, Markovits Tibor, Szalóki Dezső, Tomcsányi Péter, Varga Antal
  URI STRING  
/show/116/F-B-C
  CLASS/METHOD  
show/index
  MEMORY USAGE  
617,360 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0015
Controller Execution Time ( Show / Index )  0.0085
Total Execution Time  0.0100
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0004   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('77a15e1a452716a125e34ec80ac4be43', '3.15.0.88', 'Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko;', 1722064591) 
0.0012   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0006   SELECT *
FROM (`experiments`)
WHERE `eid` = '116' 
0.0005   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '116' 
0.0003   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '116' 
0.0002   SELECT `name`
FROM (`materials`)
WHERE `eid` = '116' 
0.0002   SELECT `source`
FROM (`sources`)
WHERE `eid` = '116' 
0.0005   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '116' 
0.0006   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '116'