Tömegpont dinamikája » Ütközési szám mérése

Média

Filmek

Ütközési_szám

Jelenség leírása

Ha bizonyos magasságból vízszintes talajra ejtünk labdákat, akkor azok kisebb sebességgel pattannak vissza, mint a leérkezési sebességük. A visszapattanási és a leérkezési sebességük arányát nevezzük ütközési számnak.

Összeállítás

Ejtsünk le labdákat bizonyos magasságból vízszintes talajra, és mérjük meg, hogy milyen magasra pattannak vissza.

Eszközök

hosszú vonalzó vagy mérőszalag., Labdák (gumilabda, ping-pong labda, stb.)

Magyarázat

111. Ütközési szám mérése

Ejtsünk labdákat bizonyos magasságból vízszintes felületre. A labdák sohasem pattannak vissza tökéletesen rugalmasan, hanem az ütközésük részben rugalmas, részben rugalmatlan. Ezt úgy is megfogalmazhatjuk, hogy a felületre v sebességgel érkezõ labdák kv sebességgel pattannak vissza, ahol 0 < k < 1, vagyis k egy nulla és egy közé esõ szám. Ezt a számot nevezzük ütközési számnak.

Az ütközési számot meghatározhatjuk, ha megmérjük, hogy bizonyos magasságból ejtve a labdát, az mekkora magasságra pattan vissza. Legyen az elengedés magassága h1, a visszaérkezés magassága h2. A labda leérkezési sebességét jelöljük v-vel, a visszapattanási sebességét pedig kv-vel. A leérkezésre és a visszapattanásra külön-külön felírhatjuk az mechanikai energia megmaradás törvényét: mgh1 = mv2/2 és mgh2 = m (kv)2/2. Ha a második egyenletet elosztjuk az elsõvel, majd mindkét oldalból gyököt vonunk, akkor megkapjuk az ütközési számot:

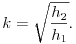
k=sqrt{frac{h_2}{h_1}}.

Felhívjuk a figyelmet arra, hogy az ütközési szám a leesõ tárgy (a mi esetünkben labda) tulajdonságai mellett a talaj mechanikai tulajdonságaitól (rugalmasságától, keménységétõl) is függ.


Szerzők

  • Baranyai Klára
  • Honyek Gyula

Forrás, irodalom, hivatkozás

  • Fizika, középiskolai tankönyvsorozat a Műszaki Kiadó gondozásában Szerzők: Gulyás János, Honyek Gyula, Markovits Tibor, Szalóki Dezső, Tomcsányi Péter, Varga Antal
  URI STRING  
/show/111/F-B-C
  CLASS/METHOD  
show/index
  MEMORY USAGE  
607,144 bytes
  BENCHMARKS  
Loading Time Base Classes  0.0003
Controller Execution Time ( Show / Index )  0.0066
Total Execution Time  0.0069
  GET DATA  
No GET data exists
  POST DATA  
No POST data exists
  DATABASE:  kiserletek   QUERIES: 9   
0.0004   INSERT INTO `sessions` (`session_id`, `ip_address`, `user_agent`, `last_activity`) VALUES ('6fee980b09beff6fdf367bb2caa830f3', '13.59.218.147', 'claudebot', 1713249925) 
0.0004   SELECT `label`, trim(item) as item
FROM (`categories`) 
0.0005   SELECT *
FROM (`experiments`)
WHERE `eid` = '111' 
0.0005   SELECT *
FROM (`exp_kwd`)
JOIN `keywords` ON `keywords`.`path`=`exp_kwd`.`path`
WHERE `eid` = '111' 
0.0005   SELECT *
FROM (`exp_cat`)
JOIN `categories` ON `categories`.`label`=`exp_cat`.`label`
WHERE `eid` = '111' 
0.0004   SELECT `name`
FROM (`materials`)
WHERE `eid` = '111' 
0.0004   SELECT `source`
FROM (`sources`)
WHERE `eid` = '111' 
0.0004   SELECT *
FROM (`exp_authors`)
JOIN `authors` ON `exp_authors`.`monogram`=`authors`.`monogram`
WHERE `exp_authors`.`eid` = '111' 
0.0005   SELECT *
FROM (`media`)
JOIN `media_type` ON `media_type`.`format`=`media`.`format`
JOIN `exp_mda` ON `media`.`mid` = `exp_mda`.`mid`
WHERE `exp_mda`.`eid` = '111'